如图所示,直角坐标系的Y轴左方为垂直纸面向里的匀强磁场,磁感应强度的大小为B.垂直x轴竖直放置一个足够大接收屏PO,它离原点距离为Og=L/2;直角坐标系的第一象限和第四象限
◎ 题目
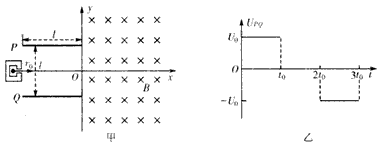
| 如图所示,直角坐标系的Y轴左方为垂直纸面向里的匀强磁场,磁感应强度的大小为B.垂直x轴竖直放置一个足够大接收屏PO,它离原点距离为Og=L/2;直角坐标系的第一象限和第四象限的abc0,Ocdf均是边长为L的正方形,其内以a、f为圆心各有一垂直纸面方向的半径为乙的1/4圆形匀强磁场区域,磁感应强度的大小均为B.bd为一线状发射装置,射出一束质量为m、电荷量为s的电子,以相同的初速度沿纸面垂直于bd边射入两个正方形区域,电子从bd边上的任意点入射,都只能从原点O射出,进入Y轴左方磁场.不考虑电子之间的相互作用,不计重力.求: (I)第一象限和第四象限中匀强磁场区域的磁感应强度的方向和电子初速度v0的大小; (2)电子打到接收屏PQ上的范围; (3)打在接收屏上的电子在磁场中运动的最长时间t.  |
◎ 答案
| (1)根据电子在第一、四象限内的偏转分析和左手定则可知: 第一象限的磁场方向为垂直纸面向外…① 第四象限的磁场方向为垂直纸面向内…② 电子从b点射入的电子从O点射出,轨迹如图所示,则: 由几何关系得其圆周运动的半径: R=L…③ 由牛顿运动定律有:ev0B=m
联解③④得:v0=
(2)设从O点沿-y方向进入磁场的电子打在屏上最低点h,圆心为O1,由图中几何关系可知:
设从O点沿某方向进入第二象限的电子其圆轨迹在i点恰与圆相切,该i点为电子打在屏上最高位置,如图所示,圆心为O2,连接O2、i交y轴为j点.由图中几何关系可知:
联解⑥⑦⑧⑨得:
|

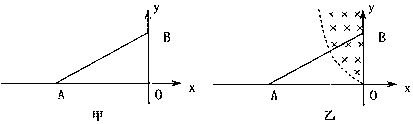
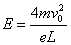

![静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44:1,如图所示,则[]A.α粒子与反冲粒子的动量](http://www.00-edu.com/d/file/2023-04-06/037384b85e1cb2b7f46c9d3cbe68861b.gif)
