如图甲所示为汤姆生在1897年测量阴极射线(电子)的比荷时所用实验装置的示意图.K为阴极,A1和A2为连接在一起的中心空透的阳极,电子从阴极发出后被电场加速,只有运动方向与A
◎ 题目
| 如图甲所示为汤姆生在1897年测量阴极射线(电子)的比荷时所用实验装置的示意图.K为阴极,A1和A2为连接在一起的中心空透的阳极,电子从阴极发出后被电场加速,只有运动方向与A1和A2的狭缝方向相同的电子才能通过,电子被加速后沿00’方向垂直进人方向互相垂直的电场、磁场的叠加区域.磁场方向垂直纸面向里,电场极板水平放置,电子在电场力和磁场力的共同作用下发生偏转.已知圆形磁场的半径为r,圆心为C. 某校物理实验小组的同学们利用该装置,进行了以下探究测量: 第一步:调节两种场的强弱.当电场强度的大小为E,磁感应强度的大小为B时,使得电子恰好能够在复合场区域内沿直线运动. 第二步:撤去电场,保持磁场和电子的速度不变,使电子只在磁场力的作用下发生偏转,打在荧屏上出现一个亮点P,通过推算得到电子的偏转角为α(CP与OO′下之间的夹角). 求:(1)电子在复合场中沿直线向右飞行的速度; (2)电子的比荷
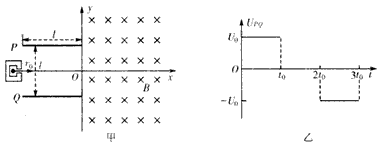
(3)有位同学提出了该装置的改造方案,把球形荧屏改成平面荧屏,并画出了如图乙的示意图.已知电场平行金属板长度为L1,金属板右则到荧屏垂直距离为L2.实验方案的第一步不变,可求出电子在复合场中沿直线向右飞行的速度.第二步撤去磁场,保持电场和电子的速度不变,使电子只在电场力的作用下发生偏转,打在荧屏上出现一个亮点P,通过屏上刻度可直接读出电子偏离屏中心点的距离
 |
◎ 答案
| (1)电子在复合场中二力平衡,即: eE=evB① 得:v=
(2)如图所示:其中R为电子在磁场中做圆(弧)运动的圆轨道半径. 所以:θ=
tanθ=
又因:evB=m
联解以上②③④⑤式得:
(3)此方案可行,原因如下. 如图设电子在电场中偏转的侧向位移为y′,  有
电子通过水平电场的时间为:t=
电子在电场中偏转的加速度为:a= |

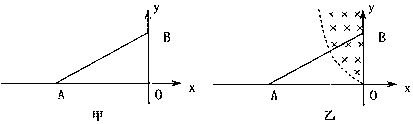
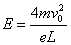

![静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44:1,如图所示,则[]A.α粒子与反冲粒子的动量](http://www.00-edu.com/d/file/2023-04-06/037384b85e1cb2b7f46c9d3cbe68861b.gif)
