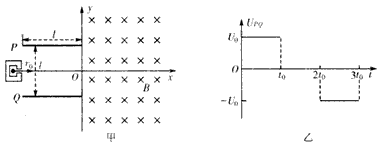
如图所示,圆形匀强磁场半径R=lcm,磁感应强度B=IT,方向垂直纸面向里,其上方有一对水平放置的平行金属板M、N,间距d=1cm,N板中央开有小孔S.小孔位于圆心0的正上方,S与O的
◎ 题目
如图所示,圆形匀强磁场半径R=lcm,磁感应强度B=IT,方向垂直纸面向里,其上方有一对水平放置的平行金属板M、N,间距d=1cm,N板中央开有小孔S.小孔位于圆心0的正上方,S与O的连线交磁场边界于A.两金属板通过导线与匝数为100匝的矩形线圈相连(为表示线圈的绕向,图中只画了2匝),线圈内有垂直纸面向里且均匀增加的磁场,穿过线圈的磁通量变化率为
(1)M、N间场强的大小和方向; (2)离子源P到A点的距离; (3)请计算说明离子进入M、N间电场后能否返回? (4)离子在磁场中运动的总时间(计算时取π=3).  |
◎ 答案
| (1)由法拉第电磁感应定律得,M、N之间的电压 U=n
M、N之间的场强大小E=
(2)离子在匀强磁场中做匀速圆周运动. 由qvB=m
解得:r=
如图所示,tanθ=
由图中的几何关系可知,离子源P到A点的距离PA=r=
(3)离子在匀强磁场中做匀速圆周运动的周期T=
离子第一次在磁场中运动的时间t1=
离子进入电场后做匀减速直线运动,在电场中运动的距离x=
a=
解得x=0.75cm<d.  因此离子不会打在M板上,会以相同的速率从A点反向再进入磁场; (4)由对称性,离子在磁场中运动的总时间: t=2t1=4×10-8s. 答:(1)M、N之间场强的大小为106N/C,方向竖直向下. (2)离子源P到A点的距离为 |

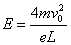

![静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44:1,如图所示,则[]A.α粒子与反冲粒子的动量](http://www.00-edu.com/d/file/2023-04-06/037384b85e1cb2b7f46c9d3cbe68861b.gif)
