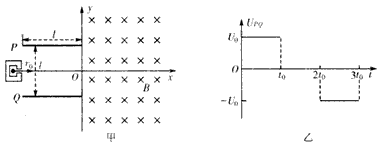
如图所示,一束质量为m、电荷量为q的带正电粒子从O点由静止开始经过匀强电场加速后,均从边界AN的中点P垂直于AN和磁场方向射入磁感应强度为B=3R2mUq的匀强磁场中.已知匀强电
解得,tE=R
|
故粒子在电磁场中运动的总时间为 t总=tE+tB=(
| π |
| 18 |
| 1 |
| 3 |
|
(2)若加速电场加速电压为U,由动能定理得:
qU=
| 1 |
| 2 |
|
在磁场中,根据牛顿第二定律得:
qv′B=m
| v′2 |
| r′ |
解得,r′=
| R |
| 3 |
分析可知粒子在磁场中运动的轨迹为一个半圆和四分之一圆周如图乙所示,
带电粒子在磁场中运动的周期为 TB=
| 2πm |
| qB |
则粒子在磁场中运动的时间为 tB′=
| 3 |
| 4 |
分析可知粒子在电场中先加速后减速再加速,由运动学公式可得:tE′=
| ||
|
|
则粒子在电场中运动的时间为3tB′=3R

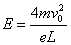

![静止在匀强磁场中的某放射性元素的原子核,当它放出一个α粒子后,其速度方向与磁场方向垂直,测得α粒子和反冲核轨道半径之比为44:1,如图所示,则[]A.α粒子与反冲粒子的动量](http://www.00-edu.com/d/file/2023-04-06/037384b85e1cb2b7f46c9d3cbe68861b.gif)
