如图(甲),在xOy平面内有足够大的勻强电场,电场方向竖直向上,电场强度E=40N/C.在_y轴左侧平面内有足够大的磁场,磁感应强度B1随时间t变化规律如图(乙)(不考虑磁场变化所产
◎ 题目
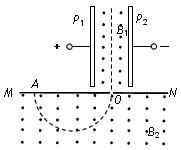
| 如图(甲),在xOy平面内有足够大的勻强电场,电场方向竖直向上,电场强度E=40N/C.在_y轴左侧平面内有足够大的磁场,磁感应强度B1随时间t变化 规律如图(乙)(不考虑磁场变化所产生电场的影响),15πs后磁场消失,选定磁 场垂直纸面向里为正方向.在y轴右侧平面内分布一个垂直纸面向外的圆形匀强磁场(图中未画出),半径r=0.3m,磁感应强度B2=0.8T,且圆的左侧与y轴始终相切.T=0 时刻,一质量m=8x104kg、电荷谓q=+2xl0-4C的微粒从x轴上xp-0.8m处的P点以 速度v=0.12m/s沿x轴正方向射入,经时间t后,从y轴上的A点进入第一象限并正对 磁场圆的圆心,穿过磁场后击中x轴上的M点.(取g=10m/s2、π=3,最终结果保留2 位有效数字)求: (1)A点的坐标yA及从P点到A点的运动时间t (2)M点的坐标×x. (3)要使微粒在圆磁场中的偏转角最大,应如何移动圆磁场?并计算出最大偏转角.  |
◎ 答案
| (1)F电=qE=8×10-3N F电=mg 所以微粒做匀速圆周运动 qvB1=m
R1=0.6m 周期T=
从乙图可知 0--5πs 匀速圆周运动R1<
微粒运行半个圆周后到点C: XC=-0.8m,yc=2R1=1.2m 5πs--10πs 向左做匀速运动,位移大小s1=v
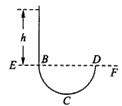
运动到D点:xD=-2.6m,yD=1.2m 10πs--15πs(s) 微粒又做匀速圆周运动 运动到E点:xE=-2.6myE=4R1=2.4m 此后微粒做匀速运动到达A点:yA=4R1=2.4m 轨迹如图所示  从P到A的时间:t=15π+tEA 或者t=2T+
所以:t≈67s (2)微粒进入圆形磁场做匀速圆周运动的半径为R2=
设轨迹圆弧对应的圆心角为θ,则tan
|