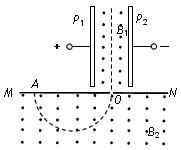
如图所示,在竖直平面内放置一长为L、内壁光滑的薄壁玻璃管,在玻璃管的a端放置一个直径比玻璃管直径略小的小球,小球带电荷量为-q、质量为m.玻璃管右边的空间存在着匀强电场
| 2mL |
| qBv0 |
水平方向位移x=v0t,得到F=
| q2B2x |
| m |
可见F是变力,而且大小随玻璃管的位移增大而均匀变化,
则F所做的功为
W=
| 1 |
| 2 |
| q2B2v0 |
| m |
|
|
(3)由于小球的重力与电场力平衡,则小球离开玻璃管后做匀速圆周运动,设半径为R,其运动轨迹如图.
t时间内玻璃管运动的距离x=v0t=v0
|
由牛顿第二定律得qvB=m
| v2 |
| R |
由几何关系得:sinα=
| x-x1 |
| R |
又
| x1 |
| R |
| vy |
| v |
则x1=
| vy |
| v |