如图所示:正方形绝缘光滑水平台面WXYZ边长l=1.8m,距地面h=0.8m.平行板电容器的极板CD间距d=0.1m且垂直放置于台面,C板位于边界WX上,D板与边界WZ相交处有一小孔.电容器外
◎ 题目
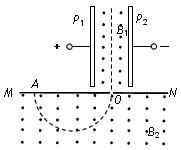
| 如图所示:正方形绝缘光滑水平台面WXYZ边长l=1.8m,距地面h=0.8m.平行板电容器的极板CD间距d=0.1m且垂直放置于台面,C板位于边界WX上,D板与边界WZ相交处有一小孔.电容器外的台面区域内有磁感应强度B=1T、方向竖直向上的匀强磁场.电荷量q=5×10-13C的微粒静止于W处,在CD间加上恒定电压U=2.5V,板间微粒经电场加速后由D板所开小孔进入磁场(微粒始终不与极板接触),然后由XY边界离开台面.在微粒离开台面瞬时,静止于X正下方水平地面上A点的滑块获得一水平速度,在微粒落地时恰好与之相遇.假定微粒在真空中运动、极板间电场视为匀强电场,滑块视为质点,滑块与地面间的动摩擦因数μ=0.2,取g=10m/s2 (1)求微粒在极板间所受电场力的大小并说明两板地极性; (2)求由XY边界离开台面的微粒的质量范围; (3)若微粒质量mo=1×10-13kg,求滑块开始运动时所获得的速度.  |
◎ 答案
(1)由左手定则及微粒的偏转方向可知,该微粒带正电,即C板为正,D板为负;电场力的大小为: F=qE=q
 (2)由题意知两个轨迹边界如图所示,由此边界结合勾股定理得:
再由向心力公式qvB=m
且qU=
联立②③④式,得该微粒的质量范围: 8.1×10-14kg<m≤2.89×10-13kg (3)将质量mo=1×10-13kg代入③④可得: v=5m/s以及R=1m,其轨迹如图所示. 由图可知cosθ=
 设微粒在空中的飞行时间为t,则由运动学公式有: h=
则滑块滑至与微粒相碰过程中微粒的水平位移为: s=vt…⑦ 微粒滑出点距左边距离: x=d+Rsinθ…⑧ 由⑤⑥⑦⑧可得: s=2m x=0.7m. 由余弦定理,知滑块的位移 S0=
由位移公式S0=v0t-
解得:v0=4.15m/s. 由正弦定理有:
得:sinφ=0.8 φ=arcsin0.8(或φ=53°) 答:(1)微粒在极板间所受电场力的大小1.25×10-11N,C板为正,D板为负. (2)由XY边界离开台面的微粒的质量范围为8.1×10-14kg<m≤2.89×10-13kg. (3)若微粒质量mo
上一篇:利用电场和磁场,可以将比荷不同的离子分开,这种方法在化学分析和原子核技术等领域有重要的应用.如图所示的矩形区域ACDG(AC边足够长)中存在垂直于纸面的匀强磁场,A处有一狭
下一篇:如图所示,虚线上方有场强为E的匀强电场,方向竖直向下,虚线上下都有磁感应强度为B的相同匀强磁场,方向垂直纸面向外.ab是一根长为l的绝缘细杆,沿电场线放置在虚线上方的场
零零教育社区:论坛热帖子
|