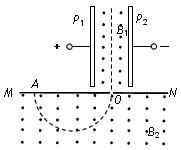
如图甲所示，空间Ⅰ区域存在方向垂直纸面向里的有界匀强磁场，左右边界线MN与PQ相互平行，MN右侧空间Ⅱ区域存在一周期性变化的匀强电场，方向沿纸面垂直MN边界，电场强度的变化规律如图乙所示（规定向左为电场的正方向）．一质量为m、电荷量为+q的粒子，在t=0时刻从电场中A点由静止开始运动，粒子重力不计．
（1）若场强大小E₁=E₂=E，A点到MN的距离为L，为使粒子进入磁场时速度最大，交变电场变化周期的最小值T₀应为多少？粒子的最大速度v₀为多大？
（2）设磁场宽度为d，改变磁感应强度B的大小，使粒子以速度v₁进入磁场后都能从磁场左边界PQ穿出，求磁感应强度B满足的条件及该粒子穿过磁场时间t的范围．
（3）若电场的场强大小E₁=2E₀，E₂=E₀，电场变化周期为T，t=0时刻从电场中A点释放的粒子经过n个周期正好到达MN边界，假定磁场足够宽，粒子经过磁场偏转后又回到电场中，向右运动的最大距离和A点到MN的距离相等．求粒子到达MN时的速度大小v和匀强磁场的磁感应强度大小B．

（1）；（2）；（3） （k=0、1、2、3……）

（16分）（1）当粒子在电场中一直做加速运动，进入磁场时速度最大，设加速时间为t，则                                         （1分）
                                                （1分）
解得                                          （1分）
由功能关系有                                  （1分）
解得                                          （1分）
（2）设粒子在磁场运动的轨道半径为r，则有
                                            （1分）
                                                  （1分）
解得                                              （1分）
根据几何关系，粒子在磁场中通过的弧长s应满足的条件是
                                            （1分）
粒子穿过磁场时间                                    （1分）
解得                                           （1分）
（3）粒子在电场变化的前半周期内加速度大小 
后半周期内加速度大小 
在一个周期内速度的增量 
经过n个周期到达MN时                              （1分）
解得                                            （1分）
粒子在磁场中运动的周期 
粒子在磁场中运动的时间                              （1分）
粒子在向右运动的最大距离和A点到MN的距离相等，说明粒子返回电场减速运动正好是前面加速的逆过程，根据对称性可知，在磁场中运动时间应满足