(19分)在竖直平面内存在如图所示的绝缘轨道,一质量为m=0.4kg、带电量为q=+0.4C的小滑块(可视为质点)在外力作用下压缩至离B点0.05m,此时弹性势能=17.25J,弹簧一端固定
◎ 题目
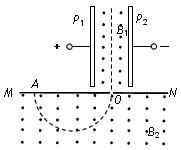
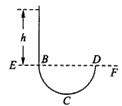
(19分)在竖直平面内存在如图所示的绝缘轨道,一质量为m=0.4kg、带电量为q=+0.4C的小滑块(可视为质点)在外力作用下压缩至离B点0.05m,此时弹性势能  =17.25J,弹簧一端固定在底端,与小滑块不相连,弹簧原长为2.05m,轨道与滑块间的动摩擦因数 =17.25J,弹簧一端固定在底端,与小滑块不相连,弹簧原长为2.05m,轨道与滑块间的动摩擦因数 .某时刻撤去外力,经过一段时间弹簧恢复至原长,再经过1.8s,同时施加电场和磁场,电场平行于纸面,且垂直x轴向上,场强E=10N/C;磁场方向垂直于纸面,且仅存在于第二、三象限内,最终滑块到达N(6m,0)点,方向与水平方向成30o斜向下.(答案可用π表示, .某时刻撤去外力,经过一段时间弹簧恢复至原长,再经过1.8s,同时施加电场和磁场,电场平行于纸面,且垂直x轴向上,场强E=10N/C;磁场方向垂直于纸面,且仅存在于第二、三象限内,最终滑块到达N(6m,0)点,方向与水平方向成30o斜向下.(答案可用π表示, ) )(1)求弹簧完全恢复瞬间,小滑块的速度; (2)求弹簧原长恢复后1.8s时小滑块所在的位置; (3)求小滑块在磁场中的运动的时间.  |
◎ 答案
(1)7.5m/s (2)小滑块此时刚好到达坐标原点(3)  s s |
◎ 解析
试题分析:(1)如图所示,弹簧释放到恢复原长经过位移s到达D点,根据能量关系,有:  (2分) (2分)其中  解得:  =7.5m/s (1分) =7.5m/s (1分) (2)此后小滑块沿斜面向上做减速运动,由牛顿第二定律得:  (2分) (2分)解得小滑块的加速度大小为:  =7.5 =7.5 (1分) (1分)设小滑块运动到E点的速度为0,上升的位移为  ,则运动时间为: ,则运动时间为: = = (1分) (1分)上升的位移为:  = = =3.75m (1分) =3.75m (1分)接着小滑块沿斜面下滑,运动时间为:  =(1.8-1)s=0.8s =(1.8-1)s=0.8s由牛顿第二定律有:  (1分) (1分)解得:  =2.5 =2.5 (1分) (1分)则下滑的位移为:  = = (1分) (1分)由图中几何关系知:BD+  =BO+ =BO+ (1分) (1分)即小滑块此时刚好到达坐标原点. (1分) (3)施加电场和磁场后,由题中数据知:  即小滑块只受洛伦兹力作用,做圆周运动到P(0,  m)点,然后做匀速直线运动运动到N(6m,0). m)点,然后做匀速直线运动运动到N(6m,0).小滑块进入磁场的速度为:  =2m/s =2m/s洛伦兹力提供向心力:  (2分) (2分)由图中几何关系知小滑块做圆周运动的半径为:r=2m (2分) 解得:  =1T (1分) =1T (1分)运动周期为:  在磁场中运动的时间为:  = = = = s (1分) s (1分)
上一篇:(12分).飞行时间质谱仪可以根据带电粒子的飞行时间对气体分子进行分析。如图所示,在真空状态下,脉冲阀P喷出微量气体,经激光照射产生不同的正离子,自a板小孔进入a、b之间
下一篇:如图所示,空间存在相互垂直的匀强电场和匀强磁场,电场的方向竖直向下,磁场方向水平(图中垂直纸面向里),一带电油滴P恰好处于静止状态,则下列说法正确的是()A.若仅撤去电
零零教育社区:论坛热帖子
|