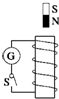
如图所示(俯视图),相距为2L的光滑平行金属导轨水平放置,导轨一部分处在以OO′为右边界的匀强磁场中,匀强磁场的磁感应强大小为B,方向垂直导轨平面向下,导轨右侧接有定值电
◎ 题目
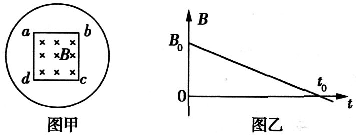
| 如图所示(俯视图),相距为2L的光滑平行金属导轨水平放置,导轨一部分处在以OO′为右边界的匀强磁场中,匀强磁场的磁感应强大小为B,方向垂直导轨平面向下,导轨右侧接有定值电阻R,导轨电阻忽略不计.在距边界OO′为L处垂直导轨放置一质量为m、电阻不计的金属杆ab.求解以下问题: (1)若金属杆ab固定在导轨上的初始位置.磁场的磁感应强度在时间t内由B均匀减小到零.求此过程中电阻R上产生的焦耳热Ql. (2)若磁场的磁感应强度不变,金属杆ab在恒力作用下由静止开始向右运动3L距离,其V--X的关系图象如图乙所示.求: ①金属杆ab刚要离开磁场时的加速度大小; ②此过程中电阻R上产生的焦耳热Q2.  |
◎ 答案
(1)磁场的磁感应强度在时间t内由B均匀减小到零,说明
根据法拉第电磁感应定律得出此过程中的感应电动势为: E1=
通过R的电流为I1=
此过程中电阻R上产生的焦耳热为Q1=I12Rt ③ 联立求得Q1=
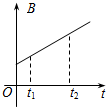
(2)①ab杆离起始位置的位移从L到3L的过程中,由动能定理可得: F(3L-L)=
ab杆刚要离开磁场时,感应电动势 E2=2BLv1 ⑤ 通过R的电流为I2=
ab杆水平方向上受安培力F安和恒力F作用,安培力为: F安=2BI2L ⑦ 联立⑤⑥⑦F安=
由牛顿第二定律可得:F-F安=ma ⑨ 联立④⑧⑨解得a=
②ab杆在磁场中由起始位置到发生位移L的过程中,由动能定理可得: FL+W安=
W安=
根据功能关系知道克服安培力做功等于电路中产生的焦耳热, 所以联立④⑩解得 Q2=-W安= |