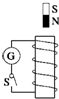
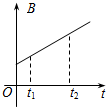
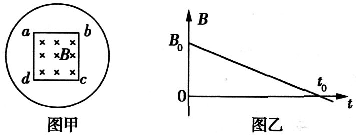
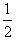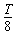如图所示,电阻不计的两光滑金属导轨相距L,放在水平绝缘桌面上,半径为R的l/4圆弧部分处在竖直平面内,水平直导轨部分处在磁感应强度为B,方向竖直向下的匀强磁场中,末端与
◎ 题目
| 如图所示,电阻不计的两光滑金属导轨相距L,放在水平绝缘桌面上,半径为R的l/4圆弧部分处在竖直平面内,水平直导轨部分处在磁感应强度为B,方向竖直向下的匀强磁场中,末端与桌面边缘平齐.两金属棒ab、cd垂直于两导轨且与导轨接触良好.棒ab质量为2m,电阻为r,棒cd的质量为m,电阻为r.重力加速度为g.开始时棒cd静止在水平直导轨上,棒ab从圆弧顶端无初速度释放,进入水平直导轨后与棒cd始终没有接触并一直向右运动,最后两棒都离开导轨落到地面上.棒ab与棒cd落地点到桌面边缘的水平距离之比为1:3. 求: (1)棒ab滑到圆弧底部进入磁场之前的速度大小 (2)棒ab和棒cd离开导轨时的速度大小; (3)棒cd在水平导轨上的最大加速度; (4)两棒在导轨上运动过程中产生的焦耳热. 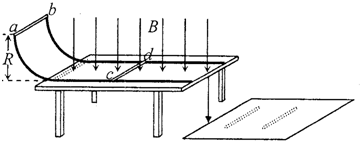 |
◎ 答案
| (1)设ab棒进入水平导轨的速度为v1,ab棒从圆弧导轨滑下机械能定恒: 2mgR=
解得:v1=
(2)离开导轨时,设ab棒的速度为
根据动量定恒得: 2mv1=2m
依题意
由平抛运动水平位移x=vt可知
联立①②③解得
(3)ab棒刚进入水平导轨时,cd棒受到的安培力最大,此时它的加速度最大,设此时回路的感应电动势为E, E=BLv ④ I=
cd棒受到的安培力为:Fcd=BIL ⑥ 根据牛顿第二定律,cd棒有最大加速度为 a= |