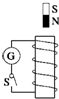
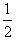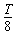如图所示，光滑且足够长的平行金属导轨MN和PQ固定在同一水平面上，两导轨间距，电阻，导轨上静止放置一质量、电阻的金属杆，导轨电阻忽略不计，整个装置处在磁感应强度的匀强磁场中，磁场的方向竖直向下，现用一外力沿水平方向拉杆，使之由静止起做匀加速运动并开始计时，若5s末杆的速度为2.5m/s，求：

（1）5s末时电阻上消耗的电功率；
（2）5s末时外力的功率.
（3）若杆最终以8m/s的速度作匀速运动,此时闭合电键S,射线源Q释放的粒子经加速电场C加速后从孔对着圆心进入半径的固定圆筒中（筒壁上的小孔只能容一个粒子通过），圆筒内有垂直水平面向下的磁感应强度为的匀强磁场。粒子每次与筒壁发生碰撞均无电荷迁移,也无机械能损失，粒子与圆筒壁碰撞5次后恰又从孔背离圆心射出,忽略粒子进入加速电场的初速度,若粒子质量,电量,则磁感应强度多大？若不计碰撞时间,粒子在圆筒内运动的总时间多大？

（1）0.1W（2）0.25W（3） 

试题分析：（1）5s末杆产生的电动势：，
电流大小为：
电阻上消耗的电功率
（2）金属棒的加速度：，由牛顿第二定律可知：
杆受的安培力大小为：
则外力F的功率：
由以上式子可得：
（3）此时回路电流强度为:
加速电场的电压为：
根据动能定理：
粒子从C孔进入磁场的速度
由题意知：粒子与圆筒壁碰撞5次后从孔离开磁场,由几何关系求得：，轨迹半径，又因为：
故：
又：，粒子作圆周运动转过的圆心角为：
根据：及
得：，粒子在圆筒内运动的总时间: