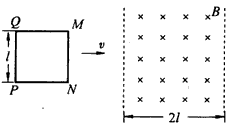
如图所示,两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上,两导轨间距为L.M、P两点间接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂
◎ 题目
| 如图所示,两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上,两导轨间距为L.M、P两点间接有阻值为R的电阻.一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直.整套装置处于匀强磁场中,磁场方向垂直于斜面向上.导轨和金属杆的电阻可忽路.让金属杆ab沿导轨由静止开始下滑,经过足够长的时间后,金属杆达到最大速度vm,在这个过程中,电阻R上产生的热量为Q.导轨和金属杆接触良好,它们之间的动摩擦因数为μ且μ<tanθ.已知重力加速度为g. (1)求磁感应强度的大小; (2)金属杆在加速下滑过程中,当速度达到v1(v1<vm)时,求此时杆的加速度大小; (3)求金属杆从静止开始至达到最大速度的过程中下降的高度.  |
◎ 答案
 (1)当ab匀速运动时,金属杆的受力图如图所示(从前向后看的视图):图中Ff为滑动摩擦力,FN为斜面支持力,F安为感应电流的安培力,mg为导体棒的重力.这时导体棒匀速直线运动,其所受的合力为零,则有: mgsinθ=Ff+F安 FN=mgcosθ, 由滑动摩擦力公式:Ff=μFN, 由安培力公式F安=BIL,由欧姆定律I=
解得:B=
(2)当导体棒的速度为v1时,由牛顿第二定律得:mgsinθ-μmgcosθ-BI'L=ma, 其中I'为速度时v1时导体棒中的感应电流,I'=
代入上式解得加速度 a=g(sinθ-μcosθ)(1-
(3)由能量守恒知,导体棒减少的重力势能,转化为动能、内能和电能,电能通过电阻R又转化为热量.所以满足: mgh=
W′=μFN?
解得金属棒下降的高度为 h=
答: (1)磁感应强度的大小为
(2)金属杆在加速下滑过程中,当速度达到v1(v1<vm
上一篇:如图所示,在空间中存在两个相邻的,磁感应强度大小相等,方向相反的有界匀强磁场,其宽度均为L.现将宽度也为L的矩形闭合线圈,从图示位置垂直于磁场方向匀速拉过磁场区域,
下一篇:如图所示,两条平行虚线之间存在匀强磁场,磁场方向垂直纸面向里,虚线间的距离为L,金属圆环的直径也为L.自圆环从左边界进入磁场开始计时,以垂直于磁场边界的恒定速度υ穿过
零零教育社区:论坛热帖子
|

![如图所示,垂直纸面的正方形匀强磁场区域内有一处于纸面的正方形导体框abcd,现将导体框分别朝①、②两个方向以v、3v速度匀速拉出磁场,则导体框从两个方向移出磁场的过程中[]](http://www.00-edu.com/d/file/2023-04-18/71b605b83ff23e89aab4e164777492a7.png)