如图所示,在磁感应强度为B=2T,方向垂直纸面向里的匀强磁场中,有一个由两条曲线状的金属导线及两电阻(图中黑点表示)组成的固定导轨,两电阻的阻值分别为R1=3Ω、R2=6Ω,两电
◎ 题目
如图所示,在磁感应强度为B=2T,方向垂直纸面向里的匀强磁场中,有一个由两条曲线状的金属导线及两电阻(图中黑点表示)组成的固定导轨,两电阻的阻值分别为R1=3Ω、R2=6Ω,两电阻的体积大小可忽略不计,两条导线的电阻忽略不计且中间用绝缘材料隔开,导轨平面与磁场垂直(位于纸面内),导轨与磁场边界(图中虚线)相切,切点为A.现有一根电阻不计、足够长的金属棒MN与磁场边界重叠,在A点对金属棒MN施加一个方向与磁场垂直、位于导轨平面内的并与磁场边界垂直的拉力F,将金属棒MN以速度v=5m/s匀速向右拉,金属棒MN与导轨接触良好,以切点为坐标原点,以F的方向为正方向建立x轴,两条导线的形状符合曲线方程y=±2
(1)推导出感应电动势e的大小与金属棒的位移x的关系式; (2)整个过程中力F所做的功; (3)从A到导轨中央的过程中通过R1的电荷量.  |
◎ 答案
(1)L=2y=4
根据法拉第电磁感应定律得: E=BLv=40
(2)因为 x=vt,所以 E=BLv=40
由于导体做匀速运动,力F所做的功等于电路中电流所做的功. 电动势有效值E′=
导体切割磁感线的时间t=
拉力F所做的功W=Q热=
(3)由E=BLv=40
|

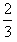
![如图所示,垂直纸面的正方形匀强磁场区域内有一处于纸面的正方形导体框abcd,现将导体框分别朝①、②两个方向以v、3v速度匀速拉出磁场,则导体框从两个方向移出磁场的过程中[]](http://www.00-edu.com/d/file/2023-04-18/71b605b83ff23e89aab4e164777492a7.png)
