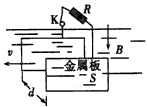
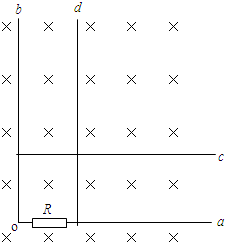
相距L=1.5m的足够长金属导轨竖直放置，质量为m1=1kg的金属棒ab和质量为m2=0.27kg的金属棒cd均通过棒两端的套环水平地套在金属导轨上，如图（a）所示，虚线上方磁场方向垂直纸
◎ 题目
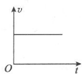
相距L=1.5m的足够长金属导轨竖直放置，质量为m1=1kg的金属棒ab和质量为m2=0.27kg的金属棒cd均通过棒两端的套环水平地套在金属导轨上，如图（a）所示，虚线上方磁场方向垂直纸面向里，虚线下方磁场方向竖直向下，两处磁场磁感应强度大小相同．ab棒光滑，cd棒与导轨间动摩擦因数为μ=0.75，两棒总电阻为1.8Ω，导轨电阻不计．ab棒在方向竖直向上，大小按图（b）所示规律变化的外力F作用下，从静止开始，沿导轨匀加速运动，同时cd棒也由静止释放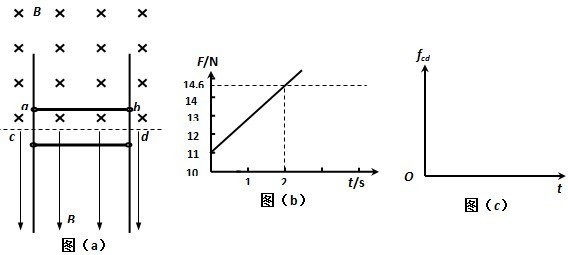． （1）指出在运动过程中ab棒中的电流方向和cd棒受到的安培力方向； （2）求出磁感应强度B的大小和ab棒加速度大小； （3）已知在2s内外力F做功40J，求这一过程中两金属棒产生的总焦耳热； （4）判断cd棒将做怎样的运动，求出cd棒达到最大速度所需的时间t0，并在图（c）中定性画出cd棒所受摩擦力fcd随时间变化的图象． |
◎ 答案
（1）在运动过程中ab棒中的电流方向向左（b→a），cd棒受到的安培力方向垂直于纸面向里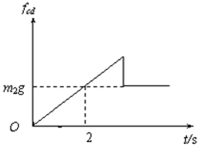．  （2）经过时间t，金属棒ab的速率v=at 此时，回路中的感应电流为I=
对金属棒ab，由牛顿第二定律得F-BIL-m1g=m1a 由以上各式整理得：F=m1a+m1g+
在图线上取两点：t1=0，F1=11N；t2=2s，F2=14.6N， 代入上式得a=1m/s2 B=1.2T （3）在2s末金属棒ab的速率vt=at=2m/s 所发生的位移s=
由动能定律得WF-m1gs-W安=
又Q=W安 联立以上方程，解得Q=WF-mgs-
（4）cd棒先做加速度逐渐减小的加速运动，当cd棒所受重力与滑动摩擦力相等时，速度达到最大；后做加速度逐渐增大的减速运动，最后停止运动． 当cd棒速度达到最大时，有m2g=μFN 又FN=F安 F安=BIL I=
整理解得t0=
fcd随时间变化的图象如图（c）所示． 答： （1）在运动过程中ab棒中的电流方向（b→a），cd棒受到的安培力方向垂直于纸面向里． （2）磁感应强度B的大小为1.2T，ab棒加速度大小为1m/s2 ． （3）已知在2s内外力F做功40J，这一过程中两金属棒产生的总焦耳热是18J； （4）cd棒的运动情况是：cd棒先做加速度逐渐减小的加速运动，当cd棒所受重力与滑动摩擦力相等时，速度达到最大；后做加速度逐渐增大的减速运动，最后停止运动．cd棒达到最大速度所需的时间t0
上一篇：如图所示，两根间距为L的金属导轨MN和PQ，电阻不计，左端弯曲部分光滑，水平部分导轨与导体棒间的滑动摩擦因数为μ，水平导轨左端有宽度为d、方向竖直向上的匀强磁场Ⅰ，右端有
下一篇：如图a，间距为d的平行金属板MN与一对光滑的平行导轨相连，平行导轨间距L=d2，一根导体棒ab以一定的初速度向右匀速运动，棒的右端存在一个垂直纸面向里，磁感应强度大小为B的
零零教育社区：论坛热帖子
|
