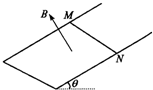
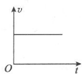
如图甲所示,足够长的平行倾斜导轨NM、PQ,两轨道间距为d,其导轨平面与水平面的夹角为θ,上端M、P之间用导线相连,处于方向垂直导轨平面斜向上的均匀变化的磁场中,磁场的磁
◎ 题目
| 如图甲所示,足够长的平行倾斜导轨NM、PQ,两轨道间距为d,其导轨平面与水平面的夹角为θ,上端M、P之间用导线相连,处于方向垂直导轨平面斜向上的均匀变化的磁场中,磁场的磁感应强度大小随时间按如图乙所示的规律变化(Bm、T已知).质量为m的导体棒ab垂直导轨放在与M、P相距为l0的位置,其与导轨间的动摩擦因数为μ(μ>tanθ).在磁感应强度从0开始不断增大以后,ab棒将从静止开始沿导轨上滑,到t1时刻(t1<T),ab棒沿导轨通过的路程为l时,其速度达到最大值.已知ab棒上滑过程中始终与导轨垂直,且接触良好,ab棒在导轨间部分的电阻为R,导轨和电线的电阻及空气阻力可忽略不计,重力加速度为g,从t=0时刻开始计时,求: (1)ab棒开始运动的时刻t0(最大静摩擦力可以认为等于滑动摩擦力); (2)在ab棒开始运动之前,通过ab棒的电荷量q; (3)ab棒达到的最大速度vm.  |
◎ 答案
| (1)ab棒开始运动时,有 FA=mgsinθ+μmgcosθ ① 由FA=BIL,I=
a在b棒开始运动的时刻t0,则有B=
联立①②③得 t0=
(2)电量q=It0,又I=
解得,q=
(3)当ab棒达到最大速度vm时,磁感应强度B=
此时电流 I=
ab棒沿斜面方向受力平衡,有 mgsinθ+μmgcosθ=BId 解得,vm= |