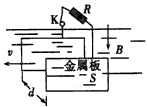
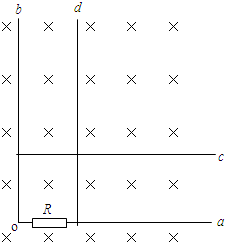
如图,两条互相平行且足够长的光滑金属导轨位于水平面内,导轨间距l=0.2m,在导轨的一端接有阻值R=3Ω的电阻,在x≥0处有一垂直水平面向下的匀强磁场,磁感强度B=0.5T.一质量
◎ 题目
| 如图,两条互相平行且足够长的光滑金属导轨位于水平面内,导轨间距l=0.2m,在导轨的 一端接有阻值R=3Ω的电阻,在x≥0处有一垂直水平面向下的匀强磁场,磁感强度B=0.5T.一质 量m=0.1kg,电阻r=2Ω的金属棒垂直搁在导轨上,并以v0=20m/s的初速度进入磁场,在水平拉 力F的作用下作持续的匀变速直线运动,加速度大小a=2m/s2、方向与初速度方向相反.棒与导轨 接触良好,其余电阻均不计.求: (1)第一次电流为零时金属棒所处的位置; (2)电流为最大值的一半时拉力F的大小及其功率; (3)金属棒开始进入磁场到速度减小为零的过程中,电阻R上产生的热量为1.6J,求该过程中拉力F所做的功.  |
◎ 答案
(1)由E=BLv,I=
若I=0,则v=0 故第一次电流为零时金属棒通过的位移为x=
(2)金属棒刚开始运动时,回路中电流最大,最大电流为 Im=
若I=
则金属棒所受的安培力为 FA=BIL=
可知FA=0.02N 讨论:①若棒向左运动,有 F1+FA=ma, 故F1=0.18N,功率P1=F1v=1.8W. ②若棒向右运动,有 F2-FA=ma, 故F2=0.22N,功率P2=F2v=2.2W. (3)设金属棒克服安培力做功为WA,拉力做功为WF. 金属棒开始进入磁场到速度减小为零的过程中,电阻R上产生的热量为QR=1.6J,金属棒产生的热量为Qr=
根据功能关系知,回路中产生的焦耳热等于金属棒克服安培力做功.则得WA=Q=
由动能定理得:WF-WA=0-
|