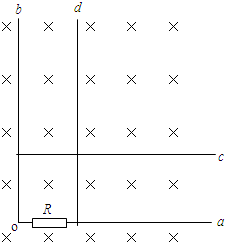
如图所示,光滑的平行金属导轨CD与EF间距为L=lm,与水平夹角为θ=30°,导轨上端用导线CE连接(导轨和连接线电阻不计),导轨处在磁感应强度为B=0.1T、方向垂直于导轨平面向上的
◎ 题目
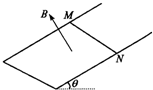
如图所示,光滑的平行金属导轨CD与EF间距为L=l m,与水平夹角为θ=30°,导轨上端用导线CE连接(导轨和连接线电阻不计),导轨处在磁感应强度为B=0.1T、方向垂直于导轨平面向上的匀强磁场中.一根电阻为R=1Ω的金属棒MN两端有导电小轮搁在两导轨上,棒上有吸水装置P.取沿导轨向下为x轴正方向,坐标原点在CE中点,开始时棒处在x=0位置(即与CE重合),棒的起始质量不计.当棒自静止起下滑时,便开始吸水,质量逐渐增大,设棒质量的增大与位移x的平方根成正比,即m=k
(1)金属棒下滑2m位移过程中,流过棒的电荷量是多少? (2)猜测金属棒下滑过程中做的是什么性质的运动,并加以证明. (3)金属棒下滑2m位移时速度为多大?  |
◎ 答案
(1)金属棒下滑1m过程中,流过棒的电量为 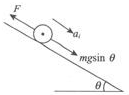 q=
(2)由于棒从静止开始运动,因此首先可以确定棒开始阶段做加速运动,然后通过受力分析,看看加速度可能如何变化. 如图所示,棒在下滑过程中沿导轨方向有向下的重力分力mgsinθ和向上的安培力F.由于m随位移x增大而增大,所以,mgsinθ是一个变力;而安培力与速度有关,也随位移增大而增大,如果两个力的差值恒定,即合外力是恒力的话,棒有可能做匀加速运动. 假设棒做的是匀加速运动,且设下滑位移x时的加速度为ax,根据牛顿第二定律,有 mgsinθ-F=max, 而安培力F=BIL=B
所以mgsinθ-
假设棒做匀加速直线运动,则瞬时速度v=
|