如图所示,间距为L的两条足够长的平行金属导轨MN,PQ与水平面夹角为a,导轨的电阻不计,导轨的N、P端连接一阻值为R的电阻,导轨置于磁感应强度大小为B、方向与导轨平面垂直的
◎ 题目
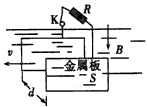
| 如图所示,间距为L的两条足够长的平行金属导轨MN,PQ与水平面夹角为a,导轨的电阻不计,导轨的N、P端连接一阻值为R的电阻,导轨置于磁感应强度大小为B、方向与导轨平面垂直的匀强磁场中.将一根质量为m、电阻为r的导体棒垂直放在导轨上,导体棒ab恰能保持静止.现给导体棒一个大小为v0、方向沿导轨平面向下的初速度,然后任其运动,导体棒在运动过程中始终保持与导轨垂直并接触良好.设导体棒所受滑动摩擦力与最大静摩擦力大小相等,求: (1)导体棒与导轨间的动摩擦因数μ; (2)在整个运动过程中电阻R上产生的焦耳热; (3)导体棒在导轨上移动的最大距离. 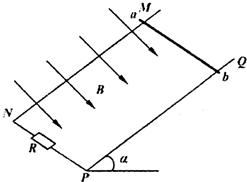 |
◎ 答案
| (1)导体棒处于平衡状态,由受力平衡得 mgsinα=μmgcosα ① 解得动摩擦因数:μ=tanα ② 故导体棒与导轨间的动摩擦因数μ=tanα. (2)导体棒在安培力作用下减速运动,最后静止在导轨上,且摩擦力所做的功和重力所做的功相等,故由能量守恒定律得整个电路中的焦耳热 Q=
由电路知识得电阻r和R串联电流时刻相等,故电阻R上的热量 QR=
故在整个运动过程中电阻R上产生的焦耳热为:QR=
(3)设导体棒在减速中的某一时刻速度为υ,取一极短时间△t,发生了一段极小的位移△x,在△t时间内,磁通量的变化量为△Φ,则有: △Φ=BL△x ⑤ 电路中的电流:I=
导体棒受到的安培力:F=BIL ⑦ △t很小,则安培力为恒力,选沿斜面方向为正方向,由动量定理 -F△t=m△v ⑧ 联立⑤⑥⑦⑧解得:-
对⑨式两边求和有:∑( -
解得导体棒下滑的总距离:x=∑△x=
故导体棒在导轨上移动的最大距离为:x=
|
◎ 解析
“略”◎ 知识点
专家分析,试题“如图所示,间距为L的两条足够长的平行金属导轨MN,PQ与水平面夹角为a,导轨的电阻不计,导轨的N、P端连接一阻值为R的电阻,导轨置于磁感应强度大小为B、方向与导轨平面垂直的…”主要考查了你对 【共点力的平衡】,【动量定理】,【导体切割磁感线时的感应电动势】,【能量守恒定律、第一类永动机】 等知识点的理解和应用能力。关于这些知识点的“档案”,你可以点击相应的链接进行查看和学习。- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
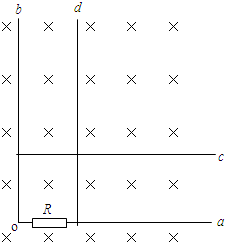
上一篇:均匀导线制成的单位正方形闭合线框abcd,每边长为L,总电阻为R,总质量为m.将其置于磁感强度为B的水平匀强磁场上方h处,如图所示.线框由静止自由下落,线框平面保持在坚直平
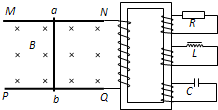
下一篇:如图甲所示,在2L≥x≥0的区域内存在着匀强磁场,磁场的方向垂直于xOy平面(纸面)向里,具有一定电阻的矩形线框abcd位于xOy平面内,线框的ab边与y轴重合,bc边长为L.令线框从t=
零零教育社区:论坛热帖子
| [家长教育] 妇产科专家告诉你:到底多大年龄,才算高龄产妇?不妨提前了解下 (2023-03-11) |
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |