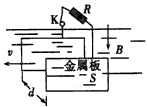
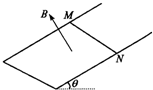
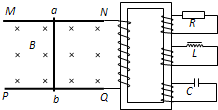
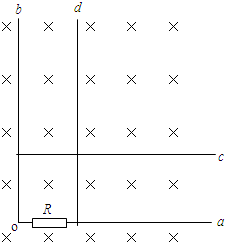
如图所示,两条平行的金属导轨相距L=lm,水平部分处在竖直向下的匀强磁场B1中,倾斜部分与水平方向的夹角为37°,处于垂直于斜面的匀强磁场B2中,两部分磁场的大小均为0.5T.
◎ 题目
| 如图所示,两条平行的金属导轨相距L=lm,水平部分处在竖直向下的匀强磁场B1中,倾斜部分与水平方向的夹角为37°,处于垂直于斜面的匀强磁场B2中,两部分磁场的大小均为0.5T.金属棒MN和PQ的质量均为m=0.2kg,电阻分别为RMN=0.5Ω和RPQ=1.5Ω.MN置于水平导轨上,与水平导轨间的动摩擦因数μ=0.5,PQ置于光滑的倾斜导轨上,两根金属棒均与导轨垂直且接触良好.从t=0时刻起,MN棒在水平外力F1的作用下由静止开始以a=2m/s2的加速度向右做匀加速直线运动,PQ则在平行于斜面方向的力F2作用下保持静止状态.不计导轨的电阻,水平导轨足够长,MN始终在水平导轨上运动.求: (1)t=5s时,PQ消耗的电功率; (2)t=0~2.0s时间内通过PQ棒的电荷量; (3)规定图示F1、F2方向作为力的正方向,分别求出F1、F2随时间t变化的函数关系; (4)若改变F1的作用规律,使MN棒的运动速度v与位移s满足关系:v=0.4s,PQ棒仍然静止在倾斜轨道上.求MN棒从静止开始到s=5m的过程中,F1所做的功.  |
◎ 答案
| (1)金属棒MN在t=5s时的速度为: v=at=2×5m/s=10m/s 电动势为: E=BLv=0.5×1×10V=5V 电流为:I=
则PQ消耗的电功率为: PPQ=I2RPQ=2.52×1.5W=9.375W (2)t=0~2.0s时间内金属棒MN运动的位移为: s=
t=0~2.0s时间内穿过回路MNQP磁通量的变化量: △φ=B1Ls=0.5×1×4Wb=2Wb t=0~2.0s时间内通过PQ棒的电荷量为: q=
(3)金属棒MN做匀加速直线运动过程中,电流为: I=
对MN运用牛顿第二定律得: F1-BIL-Ff=ma F1=ma+μmg+BIL 代入数据得:F1=(1.4+0.25t)(N) 金属棒PQ处于静止状态,根据平衡条件得: F2+BIL=mgsin37° 代入数据得:F2=(1.2-0.25t)(N) (4)MN棒做变加速直线运动,当s=5m时,vt=0.4s=0.4×5m/s=2m/s 因为速度v与位移s成正比,所以电流I、安培力也与位移s成正比,安培力做功: WB=-
|