间距为L的两条足够长的光滑平行金属导轨MN、PQ与水平面夹角为30°,导轨的电阻不计,导轨的N、Q端连接一阻值为R的电阻,导轨上有一根质量一定、电阻为r的导体棒ab垂直导轨放置
◎ 题目
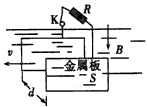
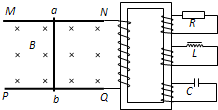
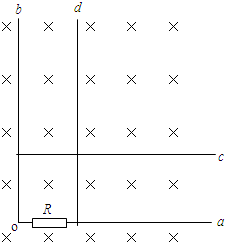
| 间距为L的两条足够长的光滑平行金属导轨MN、PQ与水平面夹角为30°,导轨的电阻不计,导轨的N、Q端连接一阻值为R的电阻,导轨上有一根质量一定、电阻为r的导体棒ab垂直导轨放置,导体棒上方距离L以上的范围存在着磁感应强度大小为B、方向与导轨平面垂直的匀强磁场.现在施加一个平行斜面向上且与棒ab重力相等的恒力,使导体棒ab从静止开始沿导轨向上运动,当ab进入磁场后,发现ab开始匀速运动,求: (1)导体棒的质量; (2)若进入磁场瞬间,拉力减小为原来的一半,求导体棒能继续向上运动的最大位移.  |
◎ 答案
| (1)导体棒从静止开始在磁场外匀加速运动距离L, 由牛顿第二定律得:F-mgsin30°=ma, 由题意可知:F=mg,解得:a=
由速度位移公式得:v2=2aL, 解得,棒进入磁场时的速度:v=
棒在磁场中受到的安培力:FB=BIL=
棒在磁场做匀速直线运动,由平衡条件得: mgsin30°+
(2)若进入磁场瞬间使拉力减半,拉力:F=
导体棒受到的安培力:FB′=BI′L=
由牛顿第二定律得:F-mgsin30°-
速度:v=
加速度:a=
由①②③得: |