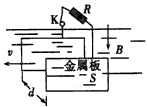
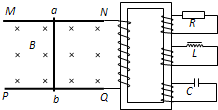
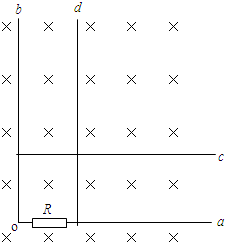
如图所示,水平放置的足够长的平行金属导轨MN、PQ的一端接有电阻R0,不计电阻的导体棒ab静置在导轨的左端MP处,并与MN垂直.以导轨PQ的左端为坐标原点O,建立直角坐标系xOy,
◎ 题目
| 如图所示,水平放置的足够长的平行金属导轨MN、PQ的一端接有电阻R0,不计电阻的导体棒ab静置在导轨的左端MP处,并与MN垂直.以导轨PQ的左端为坐标原点O,建立直角坐标系xOy,Ox轴沿PQ方向.每根导轨单位长度的电阻为r.垂直于导轨平面的非匀强磁场磁感应强度在y轴方向不变,在x轴方向上的变化规律为:B=B0+kx,并且x≥0.现在导体棒中点施加一垂直于棒的水平拉力F,使导体棒由静止开始向右做匀加速直线运动,加速度大小为a.设导体棒的质量为m,两导轨间距为L.不计导体棒与导轨间的摩擦,导体棒与导轨接触良好,不计其余部分的电阻. (1)请通过分析推导出水平拉力F的大小随横坐标x变化的关系式; (2)如果已知导体棒从x=0运动到x=x0的过程中,力F做的功为W,求此过程回路中产生的焦耳热Q; (3)若B0=0.1T,k=0.2T/m,R0=0.1Ω,r=0.1Ω/m,L=0.5m,a=4m/s2,求导体棒从x=0运动到x=1m的过程中,通过电阻R0的电荷量q.  |
◎ 答案
| (1)设导体棒运动到坐标为x处的速度为v,由法拉第电磁感应定律得产生的感应电动势为: E=BLv…① 由闭合电路欧姆定律得回路中的电流为: I=
由于棒做匀加速直线运动,所以有: v=
此时棒受到的安培力: FA=IBL…④ 由牛顿第二定律得: F-FA=ma…⑤ 由①②③④⑤联立解得:F=ma+
(2)设导体棒在x=x0处的动能为Ek,则由动能定理得: Ek=max0…⑥ 由能量守恒与转化定律得:W=Q+Ek…⑦ 将⑥式代入⑦式解得:Q=W-max0 (3)由①②两式得:I=
因为v=at,将题中所给的数值代入⑧式得:I=2t(A)… ⑨ 可知回路中的电流与时间成正比,所以在0-t时间内,通过R0的电荷量为: q=
由匀加速直线运动规律得:t=
当x=x0时,有:q=
答:(1)水平拉力F的大小随横坐标x变化的关系式为F=ma+
|