水是眼波横,山是眉峰聚。欲问行人去那边?眉眼盈盈处。才始送春归,又送君归去。若到江南赶上春,千万和春住。
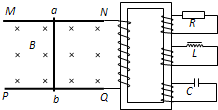
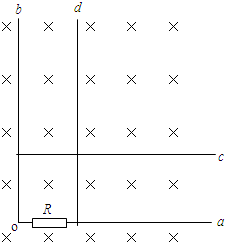
如图,相距L=1m、电阻不计的平行光滑长金属导轨固定在绝缘水平面上,两导轨左端间接有阻值R=2Ω的电阻,导轨所在足够长区域内加上与导轨所在平面垂直的匀强磁场,磁感应强度大

◎ 题目
| 如图,相距L=1m、电阻不计的平行光滑长金属导轨固定在绝缘水平面上,两导轨左端间接有阻值R=2Ω的电阻,导轨所在足够长区域内加上与导轨所在平面垂直的匀强磁场,磁感应强度大小B=1T.现有电阻r=1Ω,质量m=1kg的导体棒ab垂直导轨放置且接触良好,当导体棒ab以速度v=12m/s从边界MN进入磁场后. (1)求棒ab刚进入磁场时的加速度大小; (2)棒ab进入磁场一段距离后,速度大小变为6m/s,求从进入磁场到此时的过程中电阻R产生的焦耳热为多少; (3)求棒ab最终停的位置.  |
◎ 答案
| (1)当导体棒进入磁场切割磁感线时,导体棒受到的安培力: F=BIL=
由牛顿第二定律得:
代入数据解得:a=4m/s2; (2)对导体棒,由能量守恒定律得:
在闭合电路中:
电路中的总热量;Q=Qr+QR, 代入数据解得:QR=36J; (3)在导体棒运动的极短时间△t内,从t→△t时间内,多导体棒,由动量定理得: -F△t=m△v, 安培力:F=
则
则
上一篇:如图,在水平面(纸面)内有三根相同的均匀金属棒ab、ac和MN,其中ab、ac在a点接触,构成“V”字型导轨.空间存在垂直于纸面的均匀磁场.用力使MN向右匀速运动,从a位置开始计时,
下一篇:如图所示,等腰三角形内以底边中线为界,左右两边分布有垂直纸面向外和垂直纸面向里的等强度匀强磁场,它的底边在x轴上且长为2L,高为L.纸面内一边长为L的正方形导线框沿x轴
零零教育社区:论坛热帖子
|