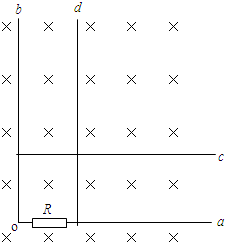
如图所示,螺线管与相距L的两竖直放置的导轨相连,导轨处于垂直纸面向外、磁感应强度为B0的匀强磁场中.金属杆ab垂直导轨,杆与导轨接触良好,并可沿导轨无摩擦滑动.螺线管横
◎ 题目
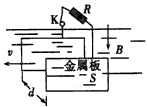
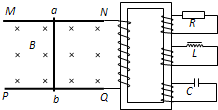
| 如图所示,螺线管与相距L的两竖直放置的导轨相连,导轨处于垂直纸面向外、磁感应强度为B0的匀强磁场中.金属杆ab垂直导轨,杆与导轨接触良好,并可沿导轨无摩擦滑动.螺线管横截面积为S,线圈匝数为N,电阻为R1,管内有水平向左的变化磁场.已知金属杆ab的质量为m,电阻为R2,重力加速度为g.不计导轨的电阻,不计空气阻力,忽略螺线管磁场对杆ab的影响. (1)为使ab杆保持静止,求通过ab的电流的大小和方向; (2)当ab杆保持静止时,求螺线管内磁场的磁感应强度B的变化率; (3)若螺线管内方向向左的磁场的磁感应强度的变化率
 |
◎ 答案
| (1)以ab为研究对象,根据平衡条件有mg=B0IL 解得:I=
根据左手定则判断可知通过ab杆电流方向为由b到a. (2)根据法拉第电磁感应定律得E=N
根据欧姆定律得I=
联立解得:
(3)根据法拉第电磁感应定律 E1=NS
ab杆切割磁感线产生的电动势E2=B0Lv 总电动势E总=E1+E2 感应电流I′=
根据牛顿第二定律mg-F=ma 安培力F=B0I′L 解得:a=g-
答: (1)为使ab杆保持静止,通过ab的电流的大小为
(2)当ab杆保持静止时,螺线管内磁场的磁感应强度B的变化率为
(3)此时杆的加速度的大小为g- |