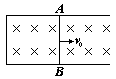
如图(甲)所示,一竖直放置的边长为L的正方形导线框,其内有垂直框面向外的均匀变化的磁场,磁场变化如图(乙)所示.导线框两端分别连平行板电容器的两极板M、N,M、N的长度和它
◎ 题目
| 如图(甲)所示,一竖直放置的边长为L的正方形导线框,其内有垂直框面向外的均匀变化的磁场,磁场变化如图(乙)所示.导线框两端分别连平行板电容器的两极板M、N,M、N的长度和它们之间的距离都是d,两平行板所在平面与纸面垂直. (1)一质子沿M、N两板正中央水平射入,恰好打在N板的中点处.已知质子的质量和电量分别为m、e,求M、N两板间的电压UMN和质子入射的初速度v0. (2)若在M、N间加一垂直纸面的匀强磁场B,质子以初速度v沿两极板的正中央入射时,恰好沿直线通过两板,求M、N间所加磁场B的大小和方向. (3)若在M、N的右侧有一垂直M、N板的长接收板P,且在接收板与M、N间也存在(2)中所加的同样大小与方向的磁场B,则质子以直线通过M、N板之后恰好没有碰到P板.求M板右端到P板的距离. 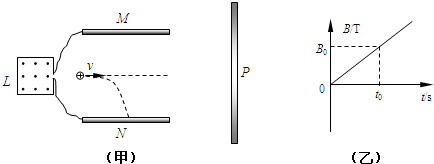 |
◎ 答案
| (1)设平行板电容器两端的电压是U, 则由法拉第电磁感应定律可得:U=
由(乙)图可知:
由①②③式解得:U=
质子在M、N间做类平抛运动,由平抛运动规律可得: 在水平方向:
在竖直方向:
由牛顿第二定律和电场力公式可得:e
由以上式子解得:v0=
(2)质子在M、N板间做匀速直线运动, 它受到电场力和洛仑兹力这一对平衡力作用. 由平衡条件得:evB=e
由⑨式解得:B=
(3)质子恰好没有碰到P板,  质子在磁场中做圆周运动的轨迹与P板相切, 由右图可知:evB=m
由几何知识知M板右端到P板的距离:S=R, 由以上两式解得S= |

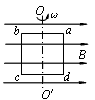
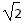

![一矩形线圈绕垂直于匀强磁场并位于线圈平面内的固定轴转动。线圈中的感应电动势e随时间t的变化规律如图所示,则下列说法中正确的是[]A.t1时刻通过线圈的磁通量为零B.t2时刻通](http://www.00-edu.com/d/file/2023-04-19/69ad69adfc44257d13a89f5bbd8112ed.gif)