濮樺瓨妲搁惇鍏煎皾濡亷绱濈仦杈ㄦЦ閻鍢查懕姘モ偓鍌涱儘闂傤喛顢戞禍鍝勫箵闁綀绔熼敍鐔烘箒閻偐娉╅惄鍫濐槱閵嗗倹澧犳慨瀣偓浣规К瑜版帪绱濋崣鍫モ偓浣告偘瑜版帒骞撻妴鍌濆閸掔増鐫欓崡妤勫垁娑撳﹥妲敍灞藉磮娑撳洤鎷伴弰銉ょ秶閵嗭拷
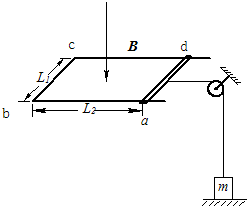
如图所示,两根足够长的固定的平行金属导轨位于同一水平面内,两导轨间的距离为L,导轨上面横放着两根导体棒ab和cd,构成矩形回路,两根导体棒的质量皆为m,电阻皆为R,回路

◎ 题目
| 如图所示,两根足够长的固定的平行金属导轨位于同一水平面内,两导轨间的距离为L,导轨上面横放着两根导体棒ab和cd,构成矩形回路,两根导体棒的质量皆为m,电阻皆为R,回路中其余部分的电阻可不计.在整个导轨平面内都有竖直向上的匀强磁场,磁感应强度为B.设两导体棒均可沿导轨无摩擦地滑行,开始时,棒cd静止,棒ab有指向棒cd的初速度v0,若两导体棒在运动中始终不接触,求: (1)在运动中产生的焦耳热最多是多少? (2)当ab棒的速度变为初速度的3/4时,cd棒的加速度是多少?  |
◎ 答案
(1)从开始到两棒达到相同速度v的过程中,两棒的总动量守恒,有 mv0=2mv,v=
根据能量守恒定律,整个过程中产生的焦耳热 Q=
在运动中产生的焦耳热最多是
(2)设ab棒的速度变为
此时回路中的电动势为 E=
此时回路中的电流为 I=
此时cd棒所受的安培力为 F=BIL=
由牛顿第二定律可得,cd棒的加速度a=鐡掑懎绔舵笟鍨焺鎼存ぞ绗呴崡鏇氱喘閹拷 濮e繐銇夋0鍡楀絿閸掝偊鏁婃潻鍥风礉閸楁洖宕熸导妯诲劕娴滎偂绗夐崑锟�
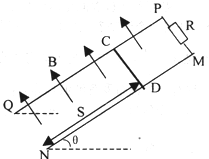
上一篇:如图1所示,空间存在B=0.5T,方向竖直向下的匀强磁场,MN、PQ是水平放置的平行长直导轨,其间距L=0.2m,R是接在导轨一端的电阻,ab是跨接在导轨上质量m=0.1kg的导体棒.从
下一篇:如图所示,虚线框abcd内为一矩形匀强磁场区域,ab=2bc,磁场方向垂直于纸面;实线框a′b′c′d′是一正方形导线框,a′b′边与ab边平行.若将导线框匀速地拉离磁场区域,以W1表示沿
零零教育社区:论坛热帖子
|