如图所示,MNPQ是一个足够长的处于竖直平面内的固定的金属框架,框架的宽度为L,电阻忽略不计.ab是一根质量为m,有一定电阻的导体,能紧贴框架无摩擦下滑,整个框架平面处于
◎ 题目
| 如图所示,MNPQ是一个足够长的处于竖直平面内的固定的金属框架,框架的宽度为L,电阻忽略不计.ab是一根质量为m,有一定电阻的导体,能紧贴框架无摩擦下滑,整个框架平面处于垂直于框架平面的匀强磁场中,磁感强度为B.当单刀双掷开关S置于1位置时,导体ab恰好静止在框架的某一处.已知电源的电动势为ε,内阻为r. (1)匀强磁场的方向如何? (2)当开关S置于2位置时,导体ab由静止开始下落,试写出ab下落运动的分析过程,并用所给的物理量表达ab在下落过程中的最大速度. (3)ab达到最大速度的1/2时,其加速度大小是多大?此时ab两端的电压为多少? (4)如果ab由静止开始下落到达到最大速度所用的时间为t,下落高度为h.试推导则该过程中h和t应满足的不等式关系? 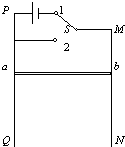 |
◎ 答案
 (1)由左手定则判断得知:磁场方向垂直纸面向内 (2)S接1时,mg=F=BIL=B
S接2时,刚开始ab下落的加速度为g,接着加速运动、同时受重力和安培力作用,由牛顿第二定律得:mg-F=ma 随着的υ的增大,感应电场也随着增大,感应电流也增大,从而使F增大而导致速度a的减小,最终达到和重力的平衡而做匀速运动,因而有:mg=F=BIL=
由①得R代入②整理后得:υm=
(3)由②可知,当ab达到最大速度的
mg-F=ma 解得,a=
又因为,ab切割磁感线产生感应电动势,其电阻相当于电源内阻,而据题意,框架电阻不计,因而外电阻为0,从而使ab两端的电压(端电压)为0. (4)作出ab运动过程的υ-t图线: ab初始加速度为g,即图线在原点的切线斜率为g.运动过程下落距离h即为图线曲线部分所包的“面积”,它介于图示“梯形面积”和“三角形面积”之间. 故有:
将(2)中求的υm值代入得:
|