如图所示,间距为L的两条足够长的平行金属导轨与水平面的夹角为θ,导轨光滑且电阻忽略不计.场强为B的条形匀强磁场方向与导轨平面垂直,磁场区域的宽度为d1,间距为d2.两根质
◎ 题目
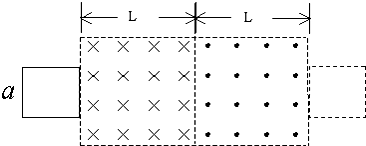
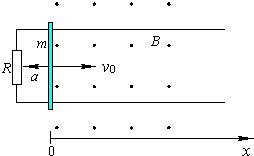
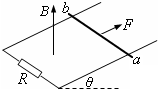
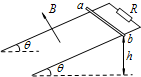
| 如图所示,间距为L的两条足够长的平行金属导轨与水平面的夹角为θ,导轨光滑且电阻忽略不计.场强为B的条形匀强磁场方向与导轨平面垂直,磁场区域的宽度为d1,间距为d2.两根质量均为m、有效电阻均为R的导体棒a和b放在导轨上,并与导轨垂直. (设重力加速度为g) (1)若a进入第2个磁场区域时,b以与a同样的速度进入第1个磁场区域,求b穿过第1个磁场区域过程中增加的动能△Ek. (2)若a进入第2个磁场区域时,b恰好离开第1个磁场区域;此后a离开第2个磁场区域时,b 又恰好进入第2个磁场区域.且a.b在任意一个磁场区域或无磁场区域的运动时间均相.求b穿过第2个磁场区域过程中,两导体棒产生的总焦耳热Q. (3)对于第(2)问所述的运动情况,求a穿出第k个磁场区域时的速率v. 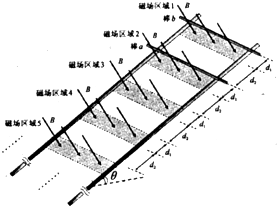 |
◎ 答案
| (1)a和b不受安培力作用,由机械能守恒知△Ek=mgd1sinθ① (2)设导体棒刚进入无磁场区域时的速度为v1,刚离开无磁场区域时的速度为v2,由能量守恒知 在磁场区域中,
在无磁场区域中
解得 Q=mg(d1+d2)sinθ ④ (3)在无磁场区域,根据匀变速直线运动规律有 v2-v1=gtsinθ⑤ 且平均速度
有磁场区域,棒a受到合力 F=mgsinθ-BIl ⑦ 感应电动势 ε=Blv ⑧ 感应电流 I=
解得 F=mgsinθ-
根据牛顿第二定律得,F=ma=m
在t到t+△t时间内
则有mgsinθ |