如图所示,质量为m的矩形线框MNPQ,MN边长为a,NP边长为b;MN边电阻为R1,PQ边电阻为R2,线框其余部分电阻不计.现将线框放在光滑绝缘的水平桌面上,PQ边与y轴重合.空间存在一
◎ 题目
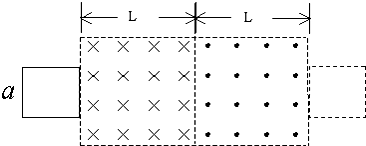
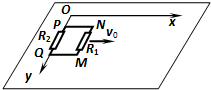
| 如图所示,质量为m的矩形线框MNPQ,MN边长为a,NP边长为b;MN边电阻为R1,PQ边电阻为R2,线框其余部分电阻不计.现将线框放在光滑绝缘的水平桌面上,PQ边与y轴重合.空间存在一个方向垂直桌面向下的磁场,该磁场的磁感应强度沿y轴方向均匀,沿x轴方向按规律Bx=B0(1-kx)变化,式中B0和k为已知常数且大于零.矩形线框以初速度v0从图示位置向x轴正方向平动.求: (1)在图示位置时线框中的感应电动势以及感应电流的大小和方向; (2)线框所受安培力的方向和安培力的表达式; (3)线框的最大运动距离xm; (4)若R1=2R2,线框运动到
 |
◎ 答案
(1)E=
I=
感应电流方向沿:NPQMN (2)线框受的安培力水平向左,安培力为: F=aI△B=
(3)根据牛顿第二定律知: F=F1-F2=m
其中m△v=-
mv0=
联立解得xm= |