如图所示,六段相互平行的金属导轨在同一水平面内,长度分别为L和2L,宽间距的导轨间相距均为2L、窄间距的导轨间相距均为L,最左端用导线连接阻值为R的电阻,各段导轨间均用
◎ 题目
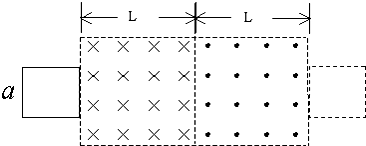
如图所示,六段相互平行的金属导轨在同一水平面内,长度分别为L和2L,宽间距的导轨间相距均为2L、窄间距的导轨间相距均为L,最左端用导线连接阻值为R的电阻,各段导轨间均用导线连接,整个装置处于方向竖直向下、磁感应强度为B的匀强磁场中.质量为m的导体棒可在各段导轨上无摩擦地滑动,在滑动过程中保持与导轨垂直.导轨和导体棒电阻均忽略不计.现使导体棒从ab位置以初速度v0垂直于导轨向右运动,则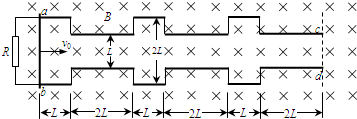 (1)若导体棒在大小为F、沿初速度方向的恒定拉力作用下运动,到达cd位置时的速度为v,求在此运动的过程中电路产生的焦耳热. (2)若导体棒在水平拉力作用下向右做匀速运动,求导体棒运动到cd位置的过程中,水平拉力做的功和电路中电流的有效值. (3)若导体棒向右运动的过程中不受拉力作用,求运动到cd位置时的速度大小. |
◎ 答案
(1)设产生的焦耳热为Q,由功能关系有9FL=Q+(
解得 Q=9FL+
(2)导体棒在宽间距和窄间距轨道上运动时,电路中产生的感应电流分别为I1=
导体棒受到的拉力分别为F1=F安=2BI1L F2=BI2L 拉力做功分别为 W1=3F1LW2=6F2L 则水平拉力做的功 W=W1+W2=
设电流的有效值为I,由功能关系有W=I2Rt 其中 t=
解得 I=
(3)设导体棒在每段宽间距和窄间距轨道上运动速度变化的大小分别为△v1和△v2,在宽间距轨道上,根据牛顿第二定律,在t~t+△t时间内有△v=
则 △v1=Σ
而△q=I△tq1= |