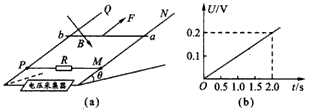
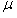如图(a)所示,一端封闭的两条平行光滑导轨相距L,距左端L处的中间一段被弯成半径为H的1/4圆弧,导轨左右两段处于高度相差H的水平面上.圆弧导轨所在区域无磁场,右段区域存在
◎ 题目
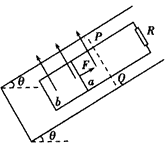
| 如图(a)所示,一端封闭的两条平行光滑导轨相距L,距左端L处的中间一段被弯成半径为H的1/4圆弧,导轨左右两段处于高度相差H的水平面上.圆弧导轨所在区域无磁场,右段区域存在磁场B0,左段区域存在均匀分布但随时间线性变化的磁场B(t),如图(b)所示,两磁场方向均竖直向上.在圆弧顶端,放置一质量为m的金属棒ab,与导轨左段形成闭合回路,从金属棒下滑开始计时,经过时间t0滑到圆弧底端.设金属棒在回路中的电阻为R,导轨电阻不计,重力加速度为g. (1)问金属棒在圆弧内滑动时,回路中感应电流的大小和方向是否发生改变?为什么? (2)求0到时间t0内,回路中感应电流产生的焦耳热量. (3)探讨在金属棒滑到圆弧底端进入匀强磁场B0的一瞬间,回路中感应电流的大小和方向. 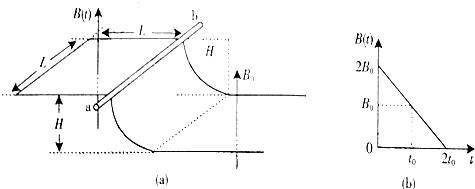 |
◎ 答案
| (1)感应电流的大小和方向均不发生改变.因为金属棒滑到圆弧任意位置时,回路中磁通量的变化率相同. (2)0-t0时间内,设回路中感应电动势大小为E0,感应电流为I,感应电流产生的焦耳热为Q,由法拉第电磁感应定律:E0=
根据闭合电路的欧姆定律:I=
有:Q=I2Rt0=
(3)设金属进入磁场B0一瞬间的速度为v,金属棒在圆弧区域下滑的过程中,机械能守恒:mgH=
在很短的时间△t内,根据法拉第电磁感应定律,金属棒进入磁场B0区域瞬间的感应电动势为E,则: E=
由闭合电路欧姆定律得:I=
解得感应电流:I=
根据上式讨论: I.当
II.当 |