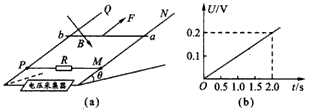
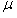如图,金属导轨间距为d,一端跨接一个电阻R,匀强磁场的磁感应强度若为B,方向垂直于平行金属导轨所在的平面,一根长金属棒与导体成θ角放置,金属棒与导轨的电阻不计,当金属
◎ 题目
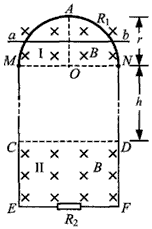
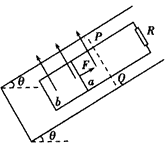
| 如图,金属导轨间距为d,一端跨接一个电阻R,匀强磁场的磁感应强度若为B,方向垂直于平行金属导轨所在的平面,一根长金属棒与导体成θ 角放置,金属棒与导轨的电阻不计,当金属棒沿垂直于棒的方向,以恒定速度v在金属导轨上滑行时,则 (1)通过电阻的电流强度为多少? (2)电阻R上发热功率为多少? (3)拉力的机械功率为多少? 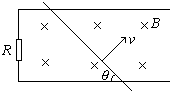 |
◎ 答案
 (1)导体棒做切割磁感线运动,导体棒两端产生感应电动势相当于闭合回路的电源,R是外电阻,电源内阻不计,由于导体棒切割磁感线时,B、L、v两两垂直,则 E=Blv 其中,L=
而电流为I=
(2)电阻R上的发热功率为电阻R的电功率,所以 PR=I2R=
(3)导体以恒定速度v运动时,导体棒受拉力F与安培力F安作用,且二力平衡,即 F=F 安=BIL=
P=Fv=
P=
也可以从能量转化守恒的关系分析,因导体匀速运动,拉力做的机械功全部转化为电能,又全部转化为焦耳热,所以 P机=P热=
答:(1)通过电阻的电流强度为
(2)电阻R上发热功率为
(3)拉力的机械功率为 |