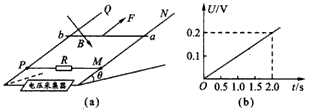
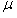如图甲所示,空间存在B=0.5T、方向竖直向下的匀强磁场,MN、PQ是处于同一水平面内相互平行的粗糙长直导轨,间距L=0.2m,R是连接在导轨一端的电阻,ab是跨接在导轨上质量为
◎ 题目
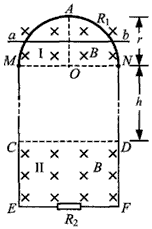
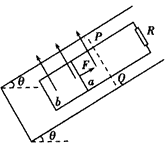
| 如图甲所示,空间存在B=0.5T、方向竖直向下的匀强磁场,MN、PQ是处于同一水平面内相互平行的粗糙长直导轨,间距L=0.2m,R是连接在导轨一端的电阻,ab是跨接在导轨上质量为m=0.1kg的导体棒.从零时刻开始,通过一小型电动机对ab棒施加一个牵引力,方向水平向左,使其从静止开始沿导轨做加速运动,此过程中棒始终保持与导轨垂直且接触良好.图乙是棒的v-t图象,其中OA段是直线,AC段是曲线,CE段是平行于t轴的直线,小型电动机在12s末达到额定功率P=4.5W,此后保持功率不变,在t=17s时,导体棒达到最大速度10m/s.除R外,其余部分电阻均不计,g=10m/s2. (1)求导体棒ab在0-12s内的加速度大小; (2)求导体棒与导轨间的动摩擦因数μ及电阻R的阻值; (3)若导体棒ab从0-17s内共发生位移102m,试求12-17s内,R上产生的焦耳热量是多少. 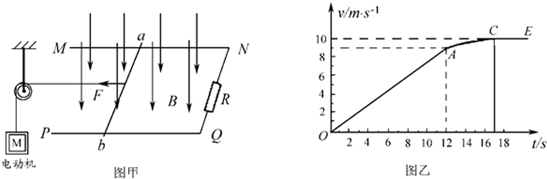 |
◎ 答案
| (1)由图象知12s末导体棒ab的速度为v1=9m/s, 在0-12s内的加速度大小为a=
(2)t1=12s时,导体棒中感应电动势为 E1=BLv1 感应电流 I1=
导体棒受到的安培力F1A=BI1L 即 F1A=
此时电动机牵引力为 F1=
由牛顿第二定律得
t2=17s时,导体棒ab的最大速度为v2=10m/s,此时加速度为零,则有
联立,代入为数据解得:μ=0.20,R=0.4Ω 摩擦因数为0.20;电阻为0.4Ω; (3)0-12s内,导体棒匀加速运动的位移 s1=
12-17s内,导体棒的位移 s2=102-54=48m 由能量守恒得 Q=Pt2-(
|