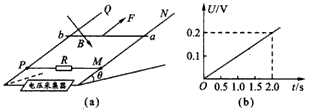
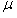如图所示,两根足够长的平行金属导轨固定放置于水平面内,导轨平面处于竖直向下的匀强磁场中,磁感应强度大小为0.3T.导轨间距为1m,导轨右端接有R=3Ω的电阻,两根完全相同的
◎ 题目
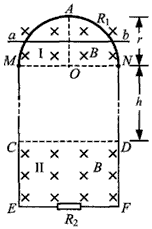
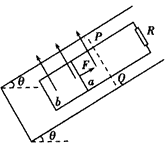
| 如图所示,两根足够长的平行金属导轨固定放置于水平面内,导轨平面处于竖直向下的匀强磁场中,磁感应强度大小为0.3T.导轨间距为1m,导轨右端接有R=3Ω的电阻,两根完全相同的导体棒L1、L2垂直跨接在导轨上,质量均为0.1kg,与导轨间的动摩擦因数均为0.25.导轨电阻不计,L1、L2在两导轨间的电阻均为3Ω.将电键S闭合,在导体棒L1上施加一个水平向左的变力F,使L1从t=0时由静止开始以2m/s2的加速度做匀加速运动.已知重力加速度为10m/s2.求: (1)变力F随时间t变化的关系式(导体棒L2尚未运动); (2)从t=0至导体棒L2由静止开始运动时所经历的时间T; (3)T时间内流过电阻R的电量q; (4)将电键S打开,最终两导体棒的速度之差△v. 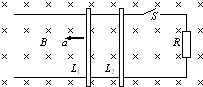 |
◎ 答案
(1)导体棒L1的速度:v=at,感应电动势E=BLv=BLat,电流I1=
R总=
对导体棒L1:F-μmg-F安1=ma 得 F-μmg-BI1L=ma 联立以上工各式得 F=0.45+0.04t (2)对导体棒L2:当安培力F安2=μmg时开始运动. F安2=BI2L,I2=
解得,T=
(3)T时间内流过L1的电量q总=
流过电阻R的电量q=
(4)S打开,两导体棒最终以相同加速度一起运动, 对导体棒L2:B
解得△v= |