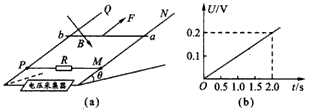
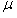如图所示,两根平行金属导轨固定在水平桌面上,每根导轨单位长度电阻为r0,导轨的端点O、O′用电阻可忽略的导线相连,两导轨间的距离为.导轨处于垂直纸面向里的非匀强磁场中,
◎ 题目
| 如图所示,两根平行金属导轨固定在水平桌面上,每根导轨单位长度电阻为r0,导轨的端点O、O′用电阻可忽略的导线相连,两导轨间的距离为.导轨处于垂直纸面向里的非匀强磁场中,磁场的磁感应强度B沿y方向大小不变,沿x方向均匀增强,即有B=kx,其中k为常数.一根质量为m、电阻不计的金属杆MN静止在坐标原点O、O′处.从t=0时刻,金属杆MN在拉力F作用下,以大小恒定为a的加速度在导轨上沿x方向无摩擦地滑动,滑动过程中杆保持与导轨垂直.求 (1)在时刻t金属杆MN产生的感应电动势大小; (2)在时刻t金属杆MN所受的外力F; (3)感应电动势的平均值与位移为x的函数关系; (4)若在时刻t撤去拉力F,试说明金属杆MN此后做什么运动,并求此后电路发出的热量.  |
◎ 答案
(1)在时刻t,有杆通过的位移大小为x=
此时B=kx=
所以在t时刻金属杆MN产生的感应电动势大小为 E=Blv=
(2)据题知,在时刻t,回路的总电阻R=2xr0=ar0t2 所以在t时刻流经回路的感应电流大小为 I=
根据右手定则判断知,感应电流方向为NMPQN(逆时针方向). 在t时刻金属杆MN所受的安培力大小为 F安=BIl 代入解得,F安=
根据牛顿第二定律得 F-F安=ma 解得 F=ma+
(3)位移为x时,杆运动的时间为△t=t=
由于B随x均匀变化,则感应电动势平均值为
根据法拉第电磁感应定律得
|