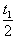濮樺瓨妲搁惇鍏煎皾濡亷绱濈仦杈ㄦЦ閻鍢查懕姘モ偓鍌涱儘闂傤喛顢戞禍鍝勫箵闁綀绔熼敍鐔烘箒閻偐娉╅惄鍫濐槱閵嗗倹澧犳慨瀣偓浣规К瑜版帪绱濋崣鍫モ偓浣告偘瑜版帒骞撻妴鍌濆閸掔増鐫欓崡妤勫垁娑撳﹥妲敍灞藉磮娑撳洤鎷伴弰銉ょ秶閵嗭拷
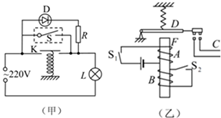
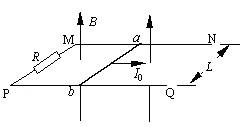
如图甲所示,两根足够长的光滑平行金属导轨相距l=0.4m,导轨平面与水平面成θ=30°角,下端通过导线连接阻值R=0.5Ω的电阻。金属棒ab阻值r=0.3Ω,质量m=0.2kg,放在两导轨上

◎ 题目
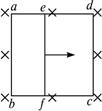
如图甲所示,两根足够长的光滑平行金属导轨相距l=0.4 m,导轨平面与水平面成θ=30°角,下端通过导线连接阻值R=0.5Ω的电阻。金属棒ab阻值r=0.3 Ω,质量m=0.2kg,放在两导轨上,与导轨垂直并保持良好接触。其余部分电阻不计,整个装置处于垂直导轨平 面向上的匀强磁场中。取g=10 m/s2。 (1)若磁场是均匀增大的匀强磁场,在开始计时即t=0时刻磁感应强度B0=2.0T,为保持金属棒静止,作用在金属棒上平行斜面向上的外力F随时间t变化的规律如图乙所示,求磁感应强度B随时间t变化的关系。 (2)若磁场是磁感应强度大小恒为B1的匀强磁场,通过额定功率P =10W的小电动机对金属棒施加平行斜面向上的牵引力,使其从静止开始沿导轨做匀加速度直线运动,经过  s电动机达到额定功率,此后电动机功率保持不变,金属棒运动的v—t图象如图丙所示。试求磁感应强度B1的大小和小电动机刚达到额定功率时金属棒的速度v1的大小? s电动机达到额定功率,此后电动机功率保持不变,金属棒运动的v—t图象如图丙所示。试求磁感应强度B1的大小和小电动机刚达到额定功率时金属棒的速度v1的大小?
|
◎ 答案
(1)2 N (2)1T ; 4m/s |
◎ 解析
(1)由于磁场均匀增大,所以金属棒中的电流I大小保持不变,安培力F安方向沿斜面向下,设任意时刻t磁感应强度为B,金属棒静止,合外力为零,则  由图乙可知在任意时刻t外力F = (2+t)N 在t=0时刻有  F0="2" N (2)由图丙可知,金属棒运动的最大速度vm=5 m/s,此时金属棒所受合力为零,设金属棒此时所受拉力大小为Fm,流过棒中的电流为Im,则 P=Fmvm… Fm-mgsinθ-B1Iml =0 Em= B1lvm  即 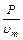 -mgsinθ- -mgsinθ- =0 =0解得 B1=1T 小电动机刚达到额定功率时,设金属棒所受拉力大小为F1,加速度大小为a,运动的速度大小为v1,流过金属棒的电流为I1,根据牛顿第二定律得 P=F1v1 v2=at… F1-mgsinθ-B1I1l =ma… E1= B1lv1  即 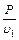 -mgsinθ- -mgsinθ-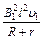 = =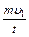 …… ……解得v1= 4m/s |
◎ 知识点
专家分析,试题“如图甲所示,两根足够长的光滑平行金属导轨相距l=0.4m,导轨平面与水平面成θ=30°角,下端通过导线连接阻值R=0.5Ω的电阻。金属棒ab阻值r=0.3Ω,质量m=0.2kg,放在两导轨上…”主要考查了你对 【电磁感应现象的综合应用】 等知识点的理解和应用能力。关于这些知识点的“档案”,你可以点击相应的链接进行查看和学习。 瓒呭競渚垮埄搴椾笅鍗曚紭鎯� 姣忓ぉ棰嗗彇鍒敊杩囷紝鍗曞崟浼樻儬浜笉鍋�- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:如图所示,在xoy平面内存在B=2T的匀强磁场,OA与OCA为置于竖直平面内的光滑金属导轨,其中OCA满足曲线方程,C为导轨的最右端,导轨OA与OCA相交处的O点和A点分别接有体积可忽
下一篇:如题18图所示,在一磁感应强度B=0.5T的匀强磁场中,垂直于磁场方向水平放置着两根相距为h=0.1m的平行金属导轨MN与PQ,导轨的电阻忽略不计.在两根导轨的端点N、Q之间连接一
零零教育社区:论坛热帖子
| [家长教育] 妇产科专家告诉你:到底多大年龄,才算高龄产妇?不妨提前了解下 (2023-03-11) |
| [高考] 2022 西安电子科技大学《软件工程》大作业答案 (2022-04-25) |
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |