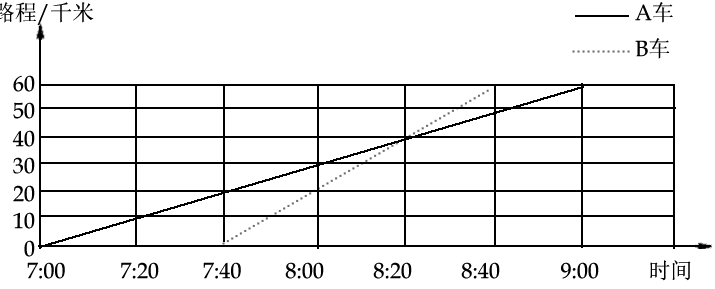
如图,LA与LB分别是根据A步行与B骑自行车在同一路上行驶的路程S与时间t的关系式所作出的图象,B出发时与A相距10千米;B骑了一段路后,自行车发生故障,进行修理;最后从起点-数学
题文
| 如图,LA与LB分别是根据A步行与B骑自行车在同一路上行驶的路程S与时间t的关系式所作出的图象,B出发时与A相距10千米;B骑了一段路后,自行车发生故障,进行修理;最后从起点出发后3小时与A相遇. (1)B修车用时______. (2)A和B的速度各是多少? (3)假设B的自行车没有发生故障,保持出发时的速度前进,多久能和A相遇?  |
答案
如图, (1)1.5-0.5=1(小时) 答:B修车用的时间是1小时; (2)(22-10)÷3 =12÷3 =4(千米/小时), 7.5÷0.5 =15(千米/小时), 答:A和B的速度分别是4千米/小时、15千米/小时; (3)设B的自行车没有发生故障,保持出发时的速度前进,x小时能和A相遇, 15x=4x+10 15x-4x=4x-4x+10, 11x=10, x=
答:假设B的自行车没有发生故障,保持出发时的速度前进,
故答案为:1小时. |
据专家权威分析,试题“如图,LA与LB分别是根据A步行与B骑自行车在同一路上行驶的路程S与..”主要考查你对 复式的折线统计图 等考点的理解。关于这些考点的“档案”如下:
复式的折线统计图
考点名称:复式的折线统计图
- 复式折线统计图:
是用一个单位长度表示一定的数量,根据数量的多少描出各点,然后把各点用线段顺次连接起来,以折线的上升或下降来表示统计数量增减变化。
折线统计图不但可以表示出数量的多少,而且还能够清楚的表示出数量增减变化的情况。
复式的折线统计图有图例,用不同颜色或形状的线条区别开来。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
上一篇:李欣和刘云为了参加学校运动会1分钟跳绳比赛,提前10天进行训练,每天测试成绩如下表(单位:次)成绩姓名12345678910李欣152155158160157159162165165167刘云1531541591551601-数学
下一篇:(20hj?广东模拟)如图是航模小组制作的两架航模飞机在一次飞行l飞行时间和高度的记录.(h)甲飞机飞行了______秒,乙飞机飞行了______秒,乙飞机的飞行时间比甲飞机短(&地九s口-数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |