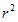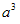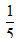在①小数的性质、②比的基本性质、③除法的性质、④商不变的性质、⑤比例的基本性质、⑥分数的基本性质这几个性质中,()三种性质是有着密切的内在联系的.A.②④⑥B.①③⑤C.①②③D.④⑤⑥-数学
题文
在①小数的性质、②比的基本性质、③除法的性质、④商不变的性质、⑤比例的基本性质、⑥分数的基本性质这几个性质中,( )三种性质是有着密切的内在联系的。
|
答案
| A |
据专家权威分析,试题“在①小数的性质、②比的基本性质、③除法的性质、④商不变的性质、⑤比..”主要考查你对 和差积商的变化规律,小数的性质,分数的基本性质,比的基本性质,比例的意义,比例的基本性质 等考点的理解。关于这些考点的“档案”如下:
和差积商的变化规律小数的性质分数的基本性质比的基本性质比例的意义,比例的基本性质
考点名称:和差积商的变化规律
- 学习目标:
理解并探索运算中蕴含的规律,并应用规律解决问题。 - 和的变化规律
(一)如果一个加数增加一个数,另一个加数不变,那么它们的和也增加同一个数。
(二)如果一个加数减少一个数,另一个加数不变,那么,它们的和也减少同一个数.
(三)如果一个加数增加一个数,另一个加数减少同样的加数,那么,它们的和不变.
(四)如果一个加数增加一个数m,另一个加数增加一个数n,那么,它们的和就增加(m+n).
(五)如果一个加数减少一个数m,另一个加数减少一个数n,那么,它们的和就减少(m+n).
(六)如果一个加数增加一个数m,另一个加数减少一个数n,当m>n时,它们的和就增加(m-n);当m<n时,它们的和就减少(n-m).
差的变化规律
(一)如果被减数增加或减少一个数,减数不变,那么它们的差也增加或减少同一个数.
(二)如果减数增加或减少一个数,被减数不变,那么,它们的差就减少或增加同一个数.
(三)如果被减数和减数同时增加或减少同一个数,那么,它们的差相等.
(四)如果被减数增加一个数m,减数减少一个数n,那么,它们的差就增加(m+n).
(五)如果被减数减少一个数m,减数增加一个数n,那么,它们的差就减少(m+n)
(六)如果被减数增加一个数m,减数增加一个数n,那么,当m>n时,它们的差就增加(m+n);当m<n时,它们的差就减少(n-m).
(七)如果被减数减少一个数m,减数减少一个数n,那么,当m>n时,它们的差要减少(m-n);当m<n时,它们的差要增加(n-m).
积的变化规律
(一)如果一个因数扩大m倍,另一个因数不变,那么,它们的积也扩大m倍.
(二)如果一个因数缩小m倍,另一个因数不变,那么,它们的积也缩小m倍.
(三)如果一个因数扩大m倍,另一个因数缩小相同的倍数,那么它们的积不变.
(四)如果一个因数扩大m倍,另一个因数扩大n倍,那么,它们的积扩大(m×n)倍.
(五)如果一个因数缩小m倍,另一个因数缩小n倍,那么,它们的积就缩小(m×n)倍.
(六)如果一个因数扩大m倍,另一个因数缩小n倍,那么,当m>n时它们的积扩大(m÷n)倍,当m<n时,它们的积就缩小(n÷m)倍.
商的变化规律
(一)如果被除数和除数同时扩大或缩小相同的倍数,那么,它们的商不变.
(二)如果被除数扩大(或缩小)m倍,除数不变,那么,它们的商就扩大(或缩小)m倍.
(三)如果除数扩大或缩小m倍,被除数不变,那么,它们的商反而缩小或扩大m倍.
(四)如果被除数扩大m倍,除数缩小n倍,那么,它们的商就扩大(m×n)倍.
(五)如果被除数缩小m倍,除数扩大n倍,那么,它们的商就缩小(m×n)倍.
(六)如果被除数扩大m倍,除数扩大n倍,当m>n时,它们的商就扩大(m÷n)倍,当m<n时,它们的商就缩小(n÷m)倍.
(七)如果被除数缩小m倍,除数缩小n倍,当m>n时,它们的商就缩小(m÷n)倍,当m<n时,它们的商就扩大(n÷m)倍.
考点名称:小数的性质
- 学习目标:
1、初步理解小数的性质。
2、能应用小数的性质化简和改写小数。 - 小数的性质:
小数的末尾添上几个“0”或者去掉几个“0”,小数的大小不变。
考点名称:分数的基本性质
考点名称:比的基本性质
- 比的基本性质:
1.比的前项和后项同时扩大或缩小相同的倍数(0除外),比值不变。
2.最简比的前项和后项互为质数,且比的前项、后项都为整数。
3.比值通常用比表示,也可以用分数(分数比)或小数表示。
4.比的后项不能为0 。
5.比的前项除以后项等于比值。
考点名称:比例的意义,比例的基本性质
- 表示两个比相等的式子叫做比例。
比例的基本性质:
组成比例的四个数,叫做比例的项。两端的两项叫做比例的外项,中间的两项叫做比例的内项。
在比例里,两个外项的积等于两个内项的积。
用字母表示为:如果 (a,b, c,d 都不等于零),那么ad=bc.
(a,b, c,d 都不等于零),那么ad=bc.
这是因为用bd去乘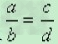 的两边,得
的两边,得 ?bd=
?bd=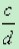 ?bd,所以ad=bc.
?bd,所以ad=bc. 性质推论:
从比例的这个基本性质,可以推得:
如果两个数的积等于另外两个数的积,那么这四个数可以组成比例。
用式子表示就是:如果ad=bc,那么 (b.d都不等于零)。
(b.d都不等于零)。
这是因为用bd 去除ad=bc两边,得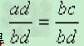 ,所以
,所以 。
。比例意义:
正比例的意义:
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量相对应的两个数的比值(也就是商)一定,这两种量就叫做成正比例的量,它们的关系叫做成正比例关系。
正比例关系两种相关联的量的变化规律:同时扩大,同时缩小,比值不变。
反比例的意义:
成反比例的量包括三个数量,一个定量和两个变量。研究两个变量之间的扩大(或缩小)的变化关系。一种量发生变化,引起另一种量发生相反的变化。这两种量是反比例的量,它们的关系成反比例关系。
反比例实质:
两种相关联的量,一种量变化,另一种量也随着变化,这两种量中相对应的两个数的积一定。这两种量叫做成反比例的量。它们的关系叫做反比例关系。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |