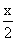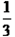列算式(或方程),并计算.(1)中国第一艘载人飞船“神舟”五号飞行轨道的近地点高度为200千米,远地点高度比近地点高度高34,“神舟”五号飞行轨道的远地点高度是多少千米?(2)一个-数学
题文
| 列算式(或方程),并计算. (1)中国第一艘载人飞船“神舟”五号飞行轨道的近地点高度为200千米,远地点高度比近地点高度高
(2)一个工厂由于采用新工艺,现在每件产品的成本是17.0元,比原来降低了15%.原来每件产品的成本是多少元? 解:设原来每件产品的成本是x元 (3)张阿姨去超市买了4千克香蕉和3.5千克苹果,共花去24.2元.已知每千克香蕉的价钱是3.6元,每千克苹果的价钱是多少元? (4)飞机的速度比火车的7倍快30千米,如果飞机每小时行450千米,那么火车每小时行多少千米? (5)某校六年级有120名师生去参观自然博物馆,某运输公司有两种车辆可供选择: ①限坐40人的大客车,每人票价5元,如满坐票价可打八折; ②限坐10人的面包车,每人票价6元,如满坐票价可按75%优惠. 请你根据以上信息为六年级师生设计一种最省钱的租车方案,并算出总租金. (6)某林场工作人员统计两棵不同树木的生长情况,并制成了它们生长情况统计图(如图).从图中可以看出: ①从开始植树到第6年,两树中生长速度较快的是______树.(填甲或乙) ②生长到第______年两树高度一样. ③第______年后,甲树长高开始减慢. ④当两树停止长高后,______树比______树高______%.  |
答案
(1)200×
=150+200, =350(千米); 答:“神舟”五号飞行轨道的远地点高度是350千米. (2)设原来每件产品的成本是x元,由题意列方程得: x×(1-15%)=17, 解这个方程得85%x=17, x=20; 答:原来每件产品的成本是20元. (3)4×3.6=14.4(元), 24.2-14.4=9.8(元), 9.8÷3.5=2.8(元); 答:每千克苹果的价钱是2.8元. (4)设火车每小时行x千米,由题意列方程得: 7x+30=450, 解这个方程得.7x=420, x=60; 答:火车每小时行420千米. (5)①若租限坐40人的大客车: 共需租金:120×5=600(元), 600×80%=480(元); ②若租限坐10人的面包车: 共需租金:120×6=720(元), 720×75%=540(元), 480<540, 租限坐40人的大客车最省钱; 需车辆数:120÷40=3(辆); 答:租限坐40人的大客车最省钱,总租金480元,需大客车3辆;. (6)从图中要以看出答案应填为①乙②10③15,④甲,乙, 第④题第三个填空(10-8)÷8×100%, =25%. 故填①乙②10③15,④甲,乙,25%. |
据专家权威分析,试题“列算式(或方程),并计算.(1)中国第一艘载人飞船“神舟”五号飞行轨..”主要考查你对 列方程解决问题 等考点的理解。关于这些考点的“档案”如下:
列方程解决问题
考点名称:列方程解决问题
- 列方程解决问题:
未知数用字母表示,参加列式。根据题意找出数量间的相等关系,列出含有未知数的等式,也就是方程。
它的优势体现在可以使未知数直接参加运算。 - 列方程解决问题一般步骤:
①审题,弄清题意:即全面分析已知数与已知数、已知数与未知数的关系。特别要把牵涉到的一些概念术语弄清,如同向,相向,增加到,增加了等。
②引进未知数:用x表示所求的数量或有关的未知量。在小学阶段所遇到的应用题并不十分复杂,一般只需要直接把要求的数量设为未知数。
③找出应用题中数量间的相等关系,列出方程。
④解方程,找出未知数的值。
⑤检验并写出答案:检验时,
一是要将所求得的未知数的值代太原方程,检验方程的解是否正确;
二是检查所求得的未知数的值是否符合题意,不符合题意的要舍去,保留符合题意的解。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
无相关信息
上一篇:哈利?波特参加数学竞赛,他一共得了68分,评分标准是:每对一道题得20分,每错一道题倒扣6分.已知他做对题的数量是做错题的2倍,并且所有的题他都做了,请问,这套试卷有多少-数学
下一篇:小亮现在的身高是1.53米,比出生时的3倍多0.03米.小亮出生时的身高是多少米?(列方程解答)-数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |