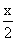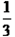题文

春风小学原计划栽种杨树、柳树和槐树共1500棵．植树开始后，当栽了杨树总数的 3 5 和30棵柳树后，又临时运来15棵槐树，这时剩下的三种树的棵数正好相等．原计划栽杨树______棵，槐树______棵，柳树______棵．

题型：解答题  难度：中档

答案

设剩下的三种树的棵数各为x棵，则已经载了杨树：x÷(1- 3 5 )× 3 5 = 3 2 x（棵）． 根据原来的总棵树，可得方程：3x+ 3 2 x+30-15=1500， 9 2 x+15=1500， 9 2 x+15-15=1500-15， 9 2 x=1485， 9 2 x× 2 9 =1485× 2 9 ， x=330； 所以原计划栽杨树：330÷（1- 3 5 ），原计划栽槐树：330-15=315（棵）； 原计划栽柳树：330+30=360（棵）； =330÷ 2 5 ， =330× 5 2 ， =825（棵）； 答：原计划栽杨树 825棵，槐树 315棵，柳树 360棵．

据专家权威分析，试题“春风小学原计划栽种杨树、柳树和槐树共1500棵．植树开始后，当栽了..”主要考查你对  列方程解决问题  等考点的理解。关于这些考点的“档案”如下：

列方程解决问题

考点名称：列方程解决问题

• 列方程解决问题：
  未知数用字母表示，参加列式。根据题意找出数量间的相等关系，列出含有未知数的等式，也就是方程。
  它的优势体现在可以使未知数直接参加运算。

• 列方程解决问题一般步骤：
  ①审题，弄清题意：即全面分析已知数与已知数、已知数与未知数的关系。特别要把牵涉到的一些概念术语弄清，如同向，相向，增加到，增加了等。
  ②引进未知数：用x表示所求的数量或有关的未知量。在小学阶段所遇到的应用题并不十分复杂，一般只需要直接把要求的数量设为未知数。
  ③找出应用题中数量间的相等关系，列出方程。
  ④解方程，找出未知数的值。
  ⑤检验并写出答案：检验时，
  一是要将所求得的未知数的值代太原方程，检验方程的解是否正确；
  二是检查所求得的未知数的值是否符合题意，不符合题意的要舍去，保留符合题意的解。