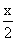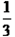有1分、2分和5分硬币共41枚,合计1.10元,其中2分币的个数比1分币多6枚.这些硬币中1分币有______个.2分币有______个,5分币有______个.-数学
题文
| 有1分、2分和5分硬币共41枚,合计1.10元,其中2分币的个数比1分币多6枚.这些硬币中1分币有______个.2分币有______个,5分币有______个. |
答案
| 1.10元=110分, 设有x枚1分币,就有(x+6)枚2分币,则有41-(x+x+6)枚5分币,由题意得, 1x+2(x+6)+5[41-(x+x+6)]=110, 1x+2x+12+5[41-2x-6]=110, 3x+12+175-10x=110, 3x-10x+187=110, 7x=77, x=11, 2分币的枚数:11+6=17(枚), 5分币的枚数:41-(2×11+6)=41-28=13(枚). 答:这些硬币中1分币有 11个.2分币有 17个,5分币有 13个. 故答案为:11,17,13. |
据专家权威分析,试题“有1分、2分和5分硬币共41枚,合计1.10元,其中2分币的个数比1分..”主要考查你对 列方程解决问题 等考点的理解。关于这些考点的“档案”如下:
列方程解决问题
考点名称:列方程解决问题
- 列方程解决问题:
未知数用字母表示,参加列式。根据题意找出数量间的相等关系,列出含有未知数的等式,也就是方程。
它的优势体现在可以使未知数直接参加运算。 - 列方程解决问题一般步骤:
①审题,弄清题意:即全面分析已知数与已知数、已知数与未知数的关系。特别要把牵涉到的一些概念术语弄清,如同向,相向,增加到,增加了等。
②引进未知数:用x表示所求的数量或有关的未知量。在小学阶段所遇到的应用题并不十分复杂,一般只需要直接把要求的数量设为未知数。
③找出应用题中数量间的相等关系,列出方程。
④解方程,找出未知数的值。
⑤检验并写出答案:检验时,
一是要将所求得的未知数的值代太原方程,检验方程的解是否正确;
二是检查所求得的未知数的值是否符合题意,不符合题意的要舍去,保留符合题意的解。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
无相关信息
上一篇:甲乙两校同时栽同样多的树.乙校栽了13后,甲校还剩下54棵没有栽;当乙校又完成剩下的34时,甲校剩下的棵数占本校要栽的总数的38,照这样计算,两校都完成任务时,一共栽树多-数学
下一篇:有粗细不同的两支蜡烛,细蜡烛的长度是粗蜡烛长度的2倍,点完细蜡烛需要l小时,点完粗蜡烛需要2小时.有一次停电,将这样两支蜡烛同时点燃,来电时,发现两支蜡烛所剩长度一样-数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |