题文

如图是一个直角等腰三角形，直角边长2厘米，图中阴影部分面积是______平方厘米．

题型：填空题  难度：偏易

答案

（1）一个圆心角为45°的扇形的面积是： 22×3.14× 45 360 =4×3.14× 45 360 =12.56× 45 360 =1.57（平方厘米）； （2）图中直角等腰三角形的面积是：2×2÷2=2（平方厘米）； （3）图中阴影部分面积是：1.57×2-2=1.14（平方厘米）； 答：图中阴影部分面积是1.14平方厘米． 故答案为：1.14．

据专家权威分析，试题“如图是一个直角等腰三角形，直角边长2厘米，图中阴影部分面积是_..”主要考查你对  三角形的周长，三角形的面积，圆的面积，重叠问题  等考点的理解。关于这些考点的“档案”如下：

三角形的周长三角形的面积圆的面积重叠问题

考点名称：三角形的周长

• 学习目标：
  1、体会理解三角形周长的概念。 
  2、学习三角形周长的计算方法。

• 三角形周长：
  三角形的周长等于三角形三边之和。
  
  周长l=a+b+c

考点名称：三角形的面积

• 学习目标：
  1、理解三角形面积公式
  2、会根据公式进行面积计算

• 图形拼组:
  1、两个完全一样的锐角三角形，可以拼成一个平行四边形。
   
  2、两个完全一样的钝角三角形，可以拼成一个平行四边形。
  
  

• 面积公式：
  三角形面积=底×高÷2，用字母表示：S=ah÷2。

考点名称：圆的面积

• 圆的面积公式：
  圆的面积=半径×半径×圆周率；
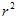  S=π（r—半径，d—直径，π—圆周率）
  圆环面积：
  外圆面积-内圆面积；
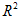  S=π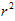-π=π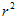（-）（R—外圆半径，r—内圆半径）

考点名称：重叠问题

• 重叠问题的解决：
  解答重叠问题要用到数学中的一个重要原理——包含与排除原理，即当两个计数部分有重复包含时，为了不重复计数，应从它们的和中排除重复部分。
  解答重叠问题的应用题，必须从条件入手进行认真的分析，有时还要画出图示，借助图形进行思考，找出哪些是重复的，重复了几次？明确求的是哪一部分，从而找出解答方法。

•