直抒胸臆:578+216=18.25-3.3=3.2-12=19×8.1=12+13=214÷3=0.99×9+0.99=214×127=112×8+112×2=21710÷7=-数学
考点名称:万以内的数的加法和减法
学习目标:
掌握竖式计算万以内数的加法,减法,用解决实际问题。- 方法点拨:
1. 万以内加法:
列竖式进行万以内的加法运算步骤:
1、列竖式;
2、相同数位一定要对齐;
3、哪一位上的数相加满十,就要向前一位进1; 如果前一位也满十,再向前一位进1;
4、写答案。
2. 万以内减法
列竖式进行万以内的减法运算步骤:
1、列竖式;
2、相同数位一定要对齐;
3、减法时,哪一位上的数不足减,向前一位借1; 如果前一位是0,再向前一位借1。
4、写答案。
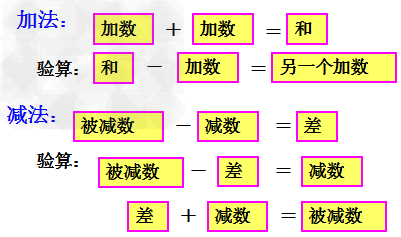
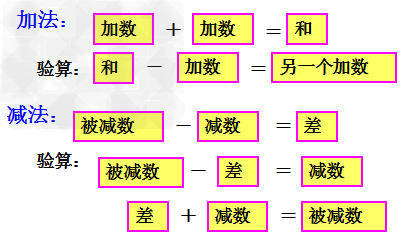
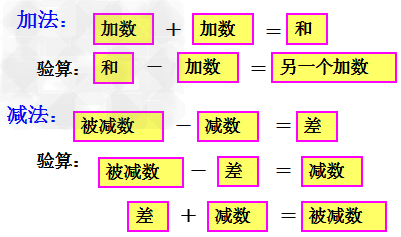
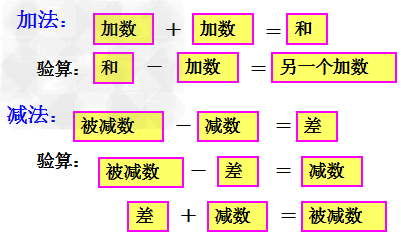
3、加减法的验算:
考点名称:小数的加法和减法
- 学习目标:
1、学习、探索小数加法和减法的计算方法。
2、理解小数点对齐的道理,掌握小数加法和减法的计算方法。 - 方法点拨:
小数加法:小数点对齐,最低位加起,满十向前一位进一。
小数减法:小数点对齐,最低位减起,不够减借1还10。
考点名称:运算定律和简便算法
- 学习目标:
1、掌握运算定律,并能运用运算定律和性质进行正确、合理、灵活的计算。
2、养成良好审题习惯,提高计算能力。 - 运算定律:
名称 内容 字母表示 用数举例 加法交换律 两个数相加,交换加数的位置,和不变。 a+b=b+a 25+14=14+25 加法结合律 三个数相加,先把前两数相加,再同第三个数相加,
或者先把后两数相加,再同第一个数相加,它们的和不变。a+b+c=
a+(b+c)20+14+36=
20+(14+36)乘法交换律 两个数相乘,交换因数的位置,它们的积不变。 a×b=b×a 10×12=12×10 乘法结合律 三个数相乘,先把前两个数相乘,再同第三个数相乘,
或者先把后两个数相乘,再同第一个数相乘,它们的积不变。a×b×c=
a×(b×c)12×25×4=
12×(25×4)乘法分配律 两个数的和同一个数相乘,可以把两个加数分别和这个
数相乘,再把两个积相加,结果不变。(a+b)×c=
a×c+b×c(12+15)×4=
12×4+15×4 - 运算性质:
名称
内容
字母表示
用数举例
减法的性质 一个数连续减去几个数等于一个数减去这几个数的和 a-b-b=
a-(b+c)250-18-52=
250-(18+52)除法的性质 一个数连续除以几个数(0除外)等于一个数除以这几个数的积 a÷b÷c=
a÷(b×c)180÷4÷25=
180÷(4×25)
考点名称:分数的加法和减法(异分母)
- 分数加、减计算法则:
①分母相同时,只把分子相加、减,分母不变;
例如1/2+3/2=(1+3)/2=4
②分母不相同时,要先通分成同分母分数再相加、减。
1/2+2/3=3/6+4/6=7/6
考点名称:分数乘法的意义和分数乘法的计算法则
- 分数乘法有两个意义:
1.分数乘以整数:和整数乘法意义相同,就是求几个相同加数的运算
2.一个数乘以分数:是求一个数的几分之几是多少
分数乘法法则:
1.分数乘整数时,用分数的分子和整数相乘的积做分子,分母不变。(要约成最简分数)
2.分数乘分数,用分子相乘的积做分子,分母相乘的积做分母,能约分的要约成最简分数(在计算中约分)。
但分子和分母不能为零。 分数与整数乘法意义:
不完全相同:
分数乘以整数的意义 就和整数乘法的意义相同;
分数乘以分数的意义 就和整数乘法的意义不相同:
乘法的意义就是求几个相同加数和的简便运算。小数乘法和分数乘法的意义之所以教材中出现两种说法(分数乘整数的意义和整数乘法的意义相同,一个数成分数的意义就是求这个数的几分之几是多少),实际上是“意义的扩展”比如:6*2/3表示6的2/3。
再在进一步理解:就是把6平均分成3份,表示这样2份的数。实际上也就是2/3个6。但基于说法不太符合常理,而改变成人们习惯的说法
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
无相关信息
上一篇:12×______=______×1.5=3÷______=______+23.-数学
下一篇:红星小学五年级有男生98人,女生112人.五年级的学生人数是六年级的79,六年级有学生多少人?-数学
零零教育社区:论坛热帖子
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![商店进528瓶饮料,卖了102瓶,大约还剩[]A.400瓶B.430瓶C.630瓶-二年级数学](http://www.00-edu.com/d/file/ks/shuxue/1/wanyineideshudejiafahejianfa/2019-02-17/4bbf76f8f1695bb7c21c8a79b516894e.png)