146+38=126-70=2.3+4.68=5.23-2.2=9÷1.5=2.25×4=30×20%=6.4÷0.8=18-19=23+29=89×34=59÷23=3-27-57=(16+23)×3=23×98×12=23×6+6×13=-数学
| 2 |
| 3 |
| 5 |
| 6 |
| 2 |
| 7 |
| 5 |
| 7 |
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 9 |
| 8 |
| 1 |
| 2 |
| 3 |
| 8 |
| 2 |
| 3 |
| 1 |
| 3 |
据专家权威分析,试题“146+38=126-70=2.3+4.68=5.23-2.2=9÷1.5=2.25×4=30×20%=6...”主要考查你对 万以内的数的加法和减法,分数的加法和减法(异分母),分数的四则混合运算及应用,分数的简便算法,百分数的计算,百分数的应用题 等考点的理解。关于这些考点的“档案”如下:
万以内的数的加法和减法分数的加法和减法(异分母)分数的四则混合运算及应用分数的简便算法百分数的计算,百分数的应用题
考点名称:万以内的数的加法和减法
学习目标:
掌握竖式计算万以内数的加法,减法,用解决实际问题。- 方法点拨:
1. 万以内加法:
列竖式进行万以内的加法运算步骤:
1、列竖式;
2、相同数位一定要对齐;
3、哪一位上的数相加满十,就要向前一位进1; 如果前一位也满十,再向前一位进1;
4、写答案。
2. 万以内减法
列竖式进行万以内的减法运算步骤:
1、列竖式;
2、相同数位一定要对齐;
3、减法时,哪一位上的数不足减,向前一位借1; 如果前一位是0,再向前一位借1。
4、写答案。
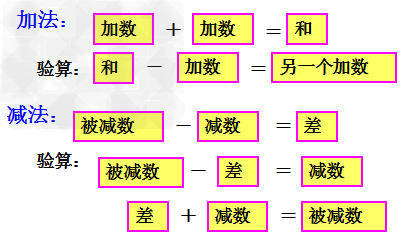
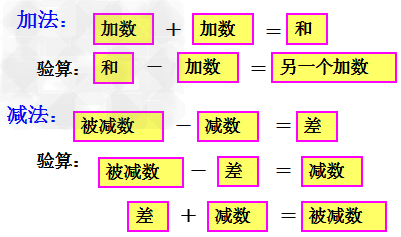
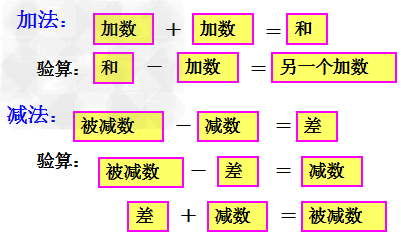
3、加减法的验算:
考点名称:分数的加法和减法(异分母)
- 分数加、减计算法则:
①分母相同时,只把分子相加、减,分母不变;
例如1/2+3/2=(1+3)/2=4
②分母不相同时,要先通分成同分母分数再相加、减。
1/2+2/3=3/6+4/6=7/6
考点名称:分数的四则混合运算及应用
运算顺序:
分数四则混合运算的运算顺序和整数则混合运算的运算顺序相同:
一个算式里,如果只含有两级运算,先算第一级运算,再算第二级运算。
在含有括号的算式里,先算小括号里面的,再算中括号里面的,最后算括号外面的。计算法则:
分数乘法的意义:
分数乘以整数 —×12 表示12个—是多少。
整数乘以真分数 12×— 表示12的—是多少。
分数乘以真分数 —×— —的—是多少。
一个数乘以带分数 —×1— 表示—的1—倍是多少。
分数加、减法的计算法则:
同分母分数相加减,分母不变,分子相加减。
异分母分数相加减,先通分,再按同分母方法计算。
分数乘除法计算方法:
分数乘法,分子相乘作分子,分母相乘作分母。
分数除法,乘以除数的倒数。分数四则运算的意义:
加法:
把两个数合并成一个数的运算 把两个小数合并成一个小数的运算 把两个分数合并成一个分数的运算;
减法:
已知两个加数的和与其中一个加数,求另一个加数的运算 已知两个加数的和与其中一个加数,求另一个加数的运算 已知两个加数的和与其中一个加数,求另一个加数的运算;
乘法:
求几个相同加数的和的简便运算,小数乘整数的意义与整数乘法意义相同;
一个数乘纯小数就是求这个数的十分之几,百分之几……
除法:
已知两个因数的积与其中一个因数,求另一个因数的运算,与整数除法的意义相同.
考点名称:分数的简便算法
- 分数的简便算法:
把整数的运算定律应用到分数中。
分数加减法运算中,同分母的先合并相加,或先相加分母互为倍数关系的,相加的和再与异分母分数正常通分相加减;
分数乘除法运算中,先通式变为乘法运算,再优先计算可以相乘得整数的分数,即分子、分母相同的两个分数。再计算剩下的。
考点名称:百分数的计算,百分数的应用题
- 常见的百分数的计算方法:

- 百分数应用题关系式:
利息的计算公式:利息=本金×利率×时间。
百分率:例:发芽率=发芽种子数÷试验种子数×100%
利率=利息÷本金×100%
折数=现价÷原价
成数=实际收成÷计划收成
税率=应纳税额÷总收入×100%
利润=售出价-成本,利润率=利润÷成本×100%=(售出价÷成本-1)×100%
折扣=实际售价÷原售价×100%(折扣<1)
浓度问题:
溶质的重量+溶剂的重量=溶液的重量;
溶质的重量÷溶液的重量×100%=浓度;
溶液的重量×浓度=溶质的重量;
溶质的重量÷浓度=溶液的重量。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![商店进528瓶饮料,卖了102瓶,大约还剩[]A.400瓶B.430瓶C.630瓶-二年级数学](http://www.00-edu.com/d/file/ks/shuxue/1/wanyineideshudejiafahejianfa/2019-02-17/4bbf76f8f1695bb7c21c8a79b516894e.png)