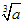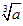学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人十分惊奇,忙问计算的奥妙.你知道怎样迅速准确的计算-数学
题文
| 学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人十分惊奇,忙问计算的奥妙.你知道怎样迅速准确的计算出结果吗?请你按下面的问题试一试: (1)103=1000,1003=1000000,你能确定59319的立方根是几位数吗?答:______位数. (2)由59319的个位数是9,你能确定59319的立方根的个位数是几吗?答:______. (3)如果划去59319后面的三位319得到数59,而33=27,43=64,由此你能确定59319的立方根的十位数是几吗?答:______.因此59319的立方根是______. (4)现在换一个数185193,你能按这种方法说出它的立方根吗? 答:①它的立方根是______位数,②它的立方根的个位数是______,③它的立方根的十位数是______,④185193的立方根是______. |
答案
| (1)103=1000,1003=1000000,你能确定59319的立方根是2位数. 故答案是:2; (2)由59319的个位数是9, 你能确定59319的立方根的个位数是 9. 故答案是9. (3)如果划去59319后面的三位319得到数59,而33=27,43=64, 由此你能确定59319的立方根的十位数是几3. 因此59319的立方根是 39. 故答案是:3,39; (4)现在换一个数185193,你能按这种方法说出它的立方根吗? ∵103=1000,1003=1000000,1000<185193<1000000, ∴185193的立方根是一个两位数, ∵185193的最后一位是3, ∴它的立方根的个位数是7, 185193去掉后3位,得到185, ∵53<185<63, ∴立方根的十位数是5, 则立方根一定是:57. 答:①它的立方根是2位数,②它的立方根的个位数是7,③它的立方根的十位数是5,④185193的立方根是57. 故答案是:2,7,5,57. |
据专家权威分析,试题“学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志..”主要考查你对 立方根 等考点的理解。关于这些考点的“档案”如下:
立方根
考点名称:立方根
- 定义:
一般地,如果一个数x的立方等于a,那么这个x叫做a的立方根。
如果一个数x的立方等于a,即x的三次方等于a(x3=a),即3个x连续相乘等于a,那么这个数x就叫做a的立方根,也叫做三次方根。
数a的立方根记作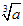 ,读作“三次根号a”。
,读作“三次根号a”。
读作:“三次根号a”其中,a叫做被开方数,3叫做根指数。(a等于所有数,包括0)如果被开方数还有指数,那么这个指数(必须是三能约去的)还可以和三次根号约去。 开立方:求一个数a的立方根的运算叫做开立方,其中a叫做被开方数。
立方根性质:
①正数的立方根是正数;负数的立方根是负数;0的立方根是0。
②一般地,如果一个数X的立方等于 a,那么这个数X就叫做a的立方根(也叫做三次方根)。
也就是说,如果x3=a,那么x叫做a的立方根。
如2是8的立方根,-3分之2是-27分之8的立方根,0是0的立方根。
③立方和开立方运算,互为逆运算。
④互为相反数的两个数的立方根也是互为相反数。
⑤负数不能开平方,但能开立方。
⑥任何数(正数、负数、或零)的立方根如果存在的话,必定只有一个。
⑦当两个数相等时,这两个数的平方根相等,反之亦然。- 平方根和立方根的关系:
区别:
⑴根指数不同:平方根的根指数为2,且可以省略不写;立方根的根指数为3,且不能省略不写。
⑵ 被开方的取值范围不同:平方根中被开方数必需为非负数;立方根中被开方数可以为任何数。
⑶ 结果不同:平方根的结果除0之外,有两个互为相反的结果;立方根的结果只有一个。
联系:
二者都是与乘方运算互为逆运算
在部分科学计算器上面需要按SHIFT键+x3才可以打出来根号。 笔算开立方的方法:
方法一
1.将被开立方数的整数部分从个位起向左每三位分为一组;
2.根据最左边一组,求得立方根的最高位数;
3.用第一组数减去立方根最高位数的立方,在其右边写上第二组数;
4.用求得的最高位数的平方的300倍试除上述余数,得出试商;并把求得的最高位数的平方的300倍与试商的积、求得的最高位数的30倍与试商的平方的积和试商的立方写在竖式左边,观察其和是否大于余数,若大于,就减小试商再试,若不大于,试商就是立方根的第二位数;
5.用同样方法继续进行下去。
方法二
第1、2步同上。
第三步,商完后,落下余数和后面紧跟着的三位,如果后面没有就把余数后面添上三个0;
第四步,将要试商的数代入式子“已商数×要试商数×(10×已商数+要试商数)×30+要商数的立方”,最接近但不超过第三步得到的数者,即为这一位要商的数。
然后重复第3、4步,直到除尽。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

![下列运算中,正确的是[]A.x2·x3=x6B.2-1=-2C.|1-π|=π-1D.-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/100/2019-04-20/cf776aba3cf359375d99e7e08b6352c9.png)