有3张不透明的卡片,除正面写有不同的实数外,其它均相同.将这三张卡片背面朝上洗匀后.第一次从中随机抽取一张,并把这张卡片上标有的实数记作第一个加数,第二次从余下的两-数学
题文
| 有3张不透明的卡片,除正面写有不同的实数外,其它均相同.将这三张卡片背面朝上洗匀后.第一次从中随机抽取一张,并把这张卡片上标有的实数记作第一个加数,第二次从余下的两张卡片中再随机抽取一张,上面标有的实数记作第二个加数. (1)写出第一次随机抽取的卡片上的实数与
(2)请你用画树状图或列表等方法,求出这两个加数可以合并的概率.  |


 会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。
会稳定在某个常数p附近,那么这个常数p就叫做事件A的概率,记作P(A)=p,概率从某种数量上刻画一个不确定事件发生的可能性的大小。 ≤1,故0≤P(A)≤1;
≤1,故0≤P(A)≤1; 。
。 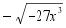
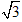
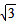
![下列二次根式中,与是同类二次根式的是[]A.B.C.D.-八年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/102/2019-04-22/bac4488c81795114c651bd251149f597.png)
![下列二次根式:①,②,③,④,其中与是同类二次根式的是[]A.①和③B.①和④C.②和④D.③和④-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/102/2019-04-22/26c100166bcf95bc8f2c44ea1ee7eef9.png)
