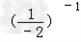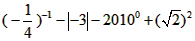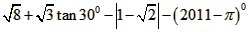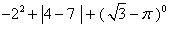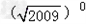计算(1)(2)-九年级数学
题文
计算
|
答案
(1)原式=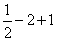 =  |
(2)  |
据专家权威分析,试题“计算(1)(2)-九年级数学-”主要考查你对 实数的运算,一元一次不等式的解法 等考点的理解。关于这些考点的“档案”如下:
实数的运算一元一次不等式的解法
考点名称:实数的运算
实数的运算:
实数包括有理数和无理数。其中无理数就是无限不循环小数,有理数就包括整数和分数。数学上,实数直观地定义为和数轴上的点一一对应的数。本来实数仅称作数,后来引入了虚数概念,原本的数称作“实数”——意义是“实在的数”。
实数可实现的基本运算有加、减、乘、除、乘方等,对非负数(即正数和0)还可以进行开方运算。实数加、减、乘、除(除数不为零)、平方后结果还是实数。任何实数都可以开奇次方,结果仍是实数,只有非负实数,才能开偶次方其结果还是实数。四则运算封闭性:
实数集R对加、减、乘、除(除数不为零)四则运算具有封闭性,即任意两个实数的和、差、积、商(除数不为零)仍然是实数。- 实数的运算法则:
1、加法法则:
(1)同号两数相加,取相同的符号,并把它们的绝对值相加;
(2)异号两数相加,取绝对值大的加数的符号,并用较大的绝对值减去较小的绝对值。
可使用
①加法交换律:两个数相加,交换加数的位置,和不变;即:a+b=b+a;
②加法结合律:三个数相加,先把前两个数相加,或先把后两个数相加,和不变;即:(a+b)+c=a+(b+c)。
2、减法法则:减去一个数等于加上这个数的相反数。即a-b=a+(-b)
3、乘法法则:
(1)两数相乘,同号取正,异号取负,并把绝对值相乘。
(2)n个实数相乘,有一个因数为0,积就为0;若n个非0的实数相乘,积的符号由负因数的个数决定,当负因数有偶数个时,积为正;当负因数为奇数个时,积为负。
(3)乘法可使用
①乘法交换律:两个数相乘,交换因数的位置,积不变,即:ab=ba;
②乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积不变,即:(ab)c=a(bc);
③分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加,即:a(b+c)=ab+ac。
4、除法法则:
(1)两数相除,同号得正,异号得负,并把绝对值相除。
(2)除以一个数等于乘以这个数的倒数。
(3)0除以任何数都等于0,0不能做被除数。
5、乘方:所表示的意义是n个a相乘,即an,正数的任何次幂是正数,负数的偶次幂是正数,负数的奇次幂是负数,乘方与开方互为逆运算。
实数的运算顺序:
乘方、开方为三级运算,乘、除为二级运算,加、减是一级运算,如果没有括号,在同一级运算中要从左到右依次运算,不同级的运算,先算高级的运算再算低级的运算,有括号的先算括号里的运算。无论何种运算,都要注意先定符号后运算。
考点名称:一元一次不等式的解法
一元一次不等式的解集:
一个有未知数的不等式的所有解,组成这个不等式的解集。例如﹕
不等式x-5≤-1的解集为x≤4;
不等式x﹥0的解集是所有正实数。
求不等式解集的过程叫做解不等式。
将不等式化为ax>b的形式
(1)若a>0,则解集为x>b/a
(2)若a<0,则解集为x<b/a一元一次不等式的特殊解:
不等式的解集一般是一个取值范围,但有时需要求未知数的某些特殊解,如求正数解、整数解、最大整数解等,解答这类问题关键是明确解的特征。- 不等式的解与解集:
不等式成立的未知数的值叫做不等式的解。如x=1是x+2>1的解
①不等式的解是指某一范围内的某个数,用它来代替不等式中的未知数,不等式成立。
②要判断某个未知数的值是不是不等式的解,可直接将该值代入等式的左、右两边,看不等式是否成立,若成立,则是;否则不是。
③一般地,一个不等式的解不止一个,往往有无数个,如所有大于3的数都是x>3的解,但也存在特殊情况,如|x|≦0,就只有一个解,为x=0
不等式的解集和不等式的解是两个不同的概念。
①不等式的解集一般是一个取值范围,在这个范围内的每一个数值都是不等式的一个解,不等式一般有无数个解。
②不等式的解集包含两方面的意思:
解集中的任何一个数值,都能使不等式成立;解集外的任何一个数值,都不能使不等式成立。(即不等式不成立)
③不等式的解集可以在数轴上直观的表示出来,如不等式x-1<2的解集是x<3,可以用数轴上表示3的点左边部分来表示,在数轴上表示3的点的位置上画空心圆圈,表示不包括这一点。 一元一次不等式的解法:
解一元一次不等式与解一元一次方程的方法步骤类似,只是在利用不等式基本性质3对不等式进行变形时,要改变不等式的符号。
有两种解题思路:
(1)可以利用不等式的基本性质,设法将未知数保留在不等式的一边,其他项在另一边;
(2)采用解一元一次方程的解题步骤:去分母、去括号、移项、合并同类项、系数化为1等步骤。
解一元一次不等式的一般顺序:
(1)去分母 (运用不等式性质2、3)
(2)去括号
(3)移项 (运用不等式性质1)
(4)合并同类项。
(5)将未知数的系数化为1 (运用不等式性质2、3)
(6)有些时候需要在数轴上表示不等式的解集
不等式解集的表示方法:
(1) 用不等式表示:一般的,一个含未知数的不等式有无数个解,其解集是一个范围,这个范围可用最简单的不等式表达出来。
例如:x-1≤2的解集是x≤3。
(2) 用数轴表示:不等式的解集可以在数轴上直观地表示出来,形象地说明不等式有无限多个解。
用数轴表示不等式的解集要注意两点:一是定边界线;二是定方向。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |