如果方程x2-4x+3=0的两个根分别是Rt△ABC的两条边,△ABC最小的角为A,那么tanA的值为______.-数学
题文
| 如果方程x2-4x+3=0的两个根分别是Rt△ABC的两条边,△ABC最小的角为A,那么tanA的值为______. |
答案
| 解方程x2-4x+3=0得, x1=1,x2=3, ①当3是直角边时,∵△ABC最小的角为A,∴tanA=
②当3是斜边时,根据勾股定理,∠A的邻边=
∴tanA=
所以tanA的值为
|
据专家权威分析,试题“如果方程x2-4x+3=0的两个根分别是Rt△ABC的两条边,△ABC最小的角为..”主要考查你对 一元二次方程的解法,勾股定理,锐角三角函数的定义 等考点的理解。关于这些考点的“档案”如下:
一元二次方程的解法勾股定理锐角三角函数的定义
考点名称:一元二次方程的解法
- 一元二次方程的解:
能够使方程左右两边相等的未知数的值叫做方程的解。
解一元二次方程方程:
求一元二次方程解的过程叫做解一元二次方程方程。 韦达定理:
一元二次方程根与系数的关系(以下两个公式很重要,经常在考试中运用到)
一般式:ax2+bx+c=0的两个根x1和x2关系:
x1+x2= -b/a
x1·x2=c/a- 一元二次方程的解法:
1、直接开平方法
利用平方根的定义直接开平方求一元二次方程的解的方法叫做直接开平方法。
直接开平方法适用于解形如 的一元二次方程,根据平方根的定义可知,x+a 是b的平方根,当
的一元二次方程,根据平方根的定义可知,x+a 是b的平方根,当 时,
时, ;当b<0时,方程没有实数根。
;当b<0时,方程没有实数根。
用直接开平方法求一元二次方程的根,一定要正确运用平方根的性质,即正数的平方根有两个,它们互为相反数,零的平方根是零,负数没有平方根。
2、配方法
配方法是一种重要的数学方法,它不仅在解一元二次方程上有所应用,而且在数学的其他领域也有着广泛的应用。
配方法的理论根据是完全平方公式 ,把公式中的a看做未知数x,并用x代替,则有
,把公式中的a看做未知数x,并用x代替,则有  。
。
3、公式法
公式法是用求根公式解一元二次方程的解的方法,它是解一元二次方程的一般方法。
一元二次方程 的求根公式:
的求根公式:
求根公式是专门用来解一元二次方程的,故首先要求a≠0;有因为开平方运算时,被开方数必须是非负数,所以第二个条件是b2-4ac≥0。即求根公式使用的前提条件是a≠0且b2-4ac≥0。
4、因式分解法
因式分解法就是利用因式分解的手段,求出方程的解的方法,这种方法简单易行,是解一元二次方程最常用的方法。
考点名称:勾股定理
- 勾股定理:
直角三角形两直角边(即“勾”,“股”)边长平方和等于斜边(即“弦”)边长的平方。也就是说,如果直角三角形的两直角边长分别为a,b,斜边长为c,那么 。
。
勾股定理只适用于直角三角形,应用于解决直角三角形中的线段求值问题。 - 定理作用
⑴勾股定理是联系数学中最基本也是最原始的两个对象——数与形的第一定理。
⑵勾股定理导致不可通约量的发现,从而深刻揭示了数与量的区别,即所谓“无理数"与有理数的差别,这就是所谓第一次数学危机。
⑶勾股定理开始把数学由计算与测量的技术转变为证明与推理的科学。
⑷勾股定理中的公式是第一个不定方程,也是最早得出完整解答的不定方程,它一方面引导到各式各样的不定方程,包括著名的费尔马大定理,另一方面也为不定方程的解题程序树立了一个范式。 - 勾股定理的应用:
数学
从勾股定理出发开平方、开立方、求圆周率等,运用勾股定理数学家还发现了无理数。
勾股定理在几何学中的实际应用非常广泛,较早的应用案例有《九章算术》中的一题:“今有池,芳一丈,薛生其中央,出水一尺,引薛赴岸,适与岸齐,问水深几何?答曰:"一十二尺"。
生活
勾股定理在生活中的应用也较广泛,举例说明如下:
1、挑选投影设备时需要选择最佳的投影屏幕尺寸。以教室为例,最佳的屏幕尺寸主要取决于使用空间的面积,从而计划好学生座位的多少和位置的安排。选购的关键则是选择适合学生的屏幕而不是选择适合投影机的屏幕,也就是说要把学生的视觉感受放在第一位。一般来说在选购时可参照三点:
第一,屏幕高度大约等于从屏幕到学生最后一排座位的距离的1/6;
第二,屏幕到第一排座位的距离应大于2倍屏幕的高度;
第三,屏幕底部应离观众席所在地面最少122厘米。
屏幕的尺寸是以其对角线的大小来定义的。一般视频图像的宽高比为4:3,教育幕为正方形。如一个72英寸的屏幕,根据勾股定理,很快就能得出屏幕的宽为1.5m,高为1.1m。
2、2005年珠峰高度复测行动。
测量珠峰的一种方法是传统的经典测量方法,就是把高程引到珠峰脚下,当精确高程传递至珠峰脚下的6个峰顶交会测量点时,通过在峰顶竖立的测量觇标,运用“勾股定理”的基本原理测定珠峰高程,配合水准测量、三角测量、导线测量等方式,获得的数据进行重力、大气等多方面改正计算,最终得到珠峰高程的有效数据。
通俗来说,就是分三步走:
第一步,先在珠峰脚下选定较容易的、能够架设水准仪器的测量点,先把这些点的精确高程确定下来;
第二步,在珠峰峰顶架起觇标,运用三角几何学中“勾股定理”的基本原理,推算出珠峰峰顶相对于这几个点的高程差;
第三步,获得的高程数据要进行重力、大气等多方面的改正计算,最终确定珠峰高程测量的有效数据。
考点名称:锐角三角函数的定义
锐角三角函数:
锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec),余割(csc)都叫做角A的锐角三角函数。
初中学习的 锐角三角函数值的定义方法是在直角三角形中定义的,所以在初中阶段求锐角的三角函数值,都是通过构造直角三角形来完成的,即把这个角放到某个直角三角形中。所谓锐角三角函数是指:我们初中研究的都是锐角的三角函数。初中研究的锐角的三角函数为:正弦(sin),余弦(cos),正切(tan)。
正弦:在直角三角形中,锐角A的对边与斜边的比叫做∠A的正弦,记作sinA,即 ;
;
余弦:在直角三角形中,锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即 ;
;
正切:在直角三角形中,锐角A的对边与邻边的比叫做∠A的正切,记作tanA,即 ,
,
锐角A的正弦、余弦、正切都叫做A的锐角三角函数。- 锐角三角函数的增减性:
1.锐角三角函数值都是正值
2.当角度在0°~90°间变化时,
正弦值随着角度的增大(或减小)而增大(或减小) ,余弦值随着角度的增大(或减小)而减小(或增大) ;
正切值随着角度的增大(或减小)而增大(或减小) ,余切值随着角度的增大(或减小)而减小(或增大);
正割值随着角度的增大(或减小)而增大(或减小),余割值随着角度的增大(或减小)而减小(或增大)。
3.当角度在0°≤A≤90°间变化时,0≤sinA≤1, 1≥cosA≥0;当角度在0°<A0, cotA>0。 锐角三角函数的关系式:
同角三角函数基本关系式
tanα·cotα=1
sin2α·cos2α=1
cos2α·sin2α=1
sinα/cosα=tanα=secα/cscα
cosα/sinα=cotα=cscα/secα
(sinα)2+(cosα)2=1
1+tanα=secα
1+cotα=cscα
诱导公式
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
cot(-α)=-cotα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
tan(π/2-α)=cotα
cot(π/2-α)=tanα
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
sin(3π/2-α)=-cosα
cos(3π/2-α)=-sinα
tan(3π/2-α)=cotα
cot(3π/2-α)=tanα
sin(3π/2+α)=-cosα
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα
cot(3π/2+α)=-tanα
sin(2π-α)=-sinα
cos(2π-α)=cosα
tan(2π-α)=-tanα
cot(2π-α)=-cotα
sin(2kπ+α)=sinα
cos(2kπ+α)=cosα
tan(2kπ+α)=tanα
cot(2kπ+α)=cotα(其中k∈Z)
二倍角、三倍角的正弦、余弦和正切公式
Sin(2α)=2sinαcosα
Cos(2α)=(cosα)2-(sinα)2=2(cosα)2-1=1-2(sinα)2
Tan(2α)=2tanα/(1-tanα)
sin(3α)=3sinα-4sin3α=4sinα·sin(60°+α)sin(60°-α)
cos(3α)=4cos3α-3cosα=4cosα·cos(60°+α)cos(60°-α)
tan(3α)=(3tanα-tan3α)/(1-3tan2α)=tanαtan(π/3+α)tan(π/3-α)
和差化积、积化和差公式
sinα+sinβ=2sin[(α+β)/2]·cos[(α-β)/2]
sinα-sinβ=2cos[(α+β)/2]·sin[(α-β)/2]
cosα+cosβ=2cos[(α+β)/2]·cos[(α-β)/2]
cosα-cosβ=-2sin[(α+β)/2]·sin[(α-β)/2]
sinαcosβ=-[sin(α+β)+sin(α-β)]
sinαsinβ=-[1][cos(α+β)-cos(α-β)]/2
cosαcosβ=[cos(α+β)+cos(α-β)]/2
sinαcosβ=[sin(α+β)+sin(α-β)]/2
cosαsinβ=[sin(α+β)-sin(α-β)]/2
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |

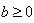
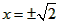
![已知x1,x2是一元二次方程ax2+bx+c=0的两根,且判别式△=b2-4ac≥0,则x1-x2的值为[]A.B.C.±D.±-九年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/107/2019-04-29/c476af9747139d34d765bbde3b2181cf.gif)
![方程2x(x-3)=5(x-3)的根为[]A、B、x=3C、D、-八年级数学](http://www.00-edu.com/d/file/ks/shuxue/2/107/2019-04-29/15503058e91de5b0952d7d7015f48c4e.png)
