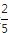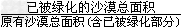如图,在矩形ABCD中,BC=20cm,P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止,已知在-九年级数学
题文
| 如图,在矩形ABCD中,BC=20cm,P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止,已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm。 (1)当x为何值时,以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边构成一个三角形; (2)当x为何值时,以P,Q,M,N为顶点的四边形是平行四边形; (3)以P,Q,M,N为顶点的四边形能否为等腰梯形?如果能,求x的值;如果不能,请说明理由。 |
 |
答案
| 解:(1)当点P与点N重合或点Q与点M重合时,以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边可能构成一个三角形, ①当点P与点N重合时, 由x2+2x=20,得x1=  ,x2=- ,x2=- (舍去), (舍去),因为BQ+CM=x+3x=  <20,此时点Q与点M不重合, <20,此时点Q与点M不重合,所以x=  符合题意, 符合题意,②当点Q与点M重合时, 由x+3x=20,得x=5, 此时DN=x2=25>20,不符合题意, 故点Q与点M不能重合,所以所求x的值为  ; ;(2)由(1)知,点Q只能在点M的左侧, ①当点P在点N的左侧时,由20-(x+3x)=20-(2x+x2), 解得x1=0(舍去),x2=2, 当x=2时四边形PQMN是平行四边形, ②当点P在点N的右侧时, 由20-(x+3x)=(2x+x2)-20, 解得x1=-10(舍去),x2=4, 当x=4时四边形NQMP是平行四边形, 所以当x=2或x=4时,以P,Q,M,N为顶点的四边形是平行四边形; (3)以P,Q,M,N为顶点的四边形不能为等腰梯形, 理由如下: 过点Q,M分别作AD的垂线,垂足分别为点E,F, 由于2x>x, 所以点E一定在点P的左侧, 若以P,Q,M,N为顶点的四边形是等腰梯形, 则点F一定在点N的右侧,且PE=NF, 即2x-x=x2-3x,解得x1=0(舍去),x2=4, 由于当x=4时,以P,Q,M,N为顶点的四边形是平行四边形, 所以以P,Q,M,N为顶点的四边形不能为等腰梯形。 |
据专家权威分析,试题“如图,在矩形ABCD中,BC=20cm,P,Q,M,N分别从A,B,C,D出发沿..”主要考查你对 一元二次方程的应用,平行四边形的判定,梯形,梯形的中位线 等考点的理解。关于这些考点的“档案”如下:
一元二次方程的应用平行四边形的判定梯形,梯形的中位线
考点名称:一元二次方程的应用
- 建立一元二次方程模型进行求解,把得到的答案带回实际问题中检验是否合理,来解决实际问题,如打折、营销、增长率问题等。
列一元二次次方程组解应用题的一般步骤:
可概括为“审、设、列、解、答”五步,即:
(1)审:是指读懂题意,弄清题意,明确哪些是已知量,哪些是未知量以及它们之间的关系;
(2)设:是指设未知数;
(3)列:就是列方程,这是非常重要的一步,一般先找出能够表达应用题全部含义的一个等量关系,然后列代数式表示等量关系中的各个量,就得到含有未知数的等式,即方程;
(4)解:解这个方程,求出两个未知数的值;
(5)答:在对求出的方程的解做出是否合理判断的基础上,写出答案。
提示:
①列方程解应用题时,要善于将普通语言化为数学语言,审题时,要特别注意关键词语,如“多、少、快、慢、和、差、倍、分、超过、剩余、增加、减少”等等,此外,还要掌握一些常用的公式或特殊的等量关系,如特殊图形的面积公式、行程问题、工程问题、增长率问题中的一些特殊关系等。
②注重解法选择与验根,在具体问题中要注意恰当的选择解法,以保证解题过程简单流畅,特别注意要对方程的解进行检验,根据实际情况作出正确取舍,以保证结论的准确性。
常见题型公式:
工程问题:
工程问题中的三个量及其关系为:工作总量=工作效率×工作时间
经常在题目中未给出工作总量时,设工作总量为单位1。利润赢亏问题
销售问题中常出现的量有:进价、售价、标价、利润等
有关关系式:
商品利润=商品售价—商品进价=商品标价×折扣率—商品进价
商品利润率=商品利润/商品进价
商品售价=商品标价×折扣率存款利率问题:
利息=本金×利率×期数
本息和=本金+利息
利息税=利息×税率(20%)行程问题:
基本数量关系:路程=速度×时间,时间=路程÷速度,速度=路程÷时间,
路程=速度×时间。
①相遇问题:快行距+慢行距=原距;
②追及问题:快行距-慢行距=原距;
③航行问题:顺水(风)速度=静水(风)速度+水流(风)速度,
逆水(风)速度=静水(风)速度-水流(风)速度
考点名称:平行四边形的判定
- 平行四边形的判定:
(1)定义:两组对边分别平行的四边形是平行四边形;
(2)定理1:两组对角分别相等的四边形是平行四边形;
(3)定理2:两组对边分别相等的四边形是平行四边形;
(4)定理3:对角线互相平分的四边形是平行四边形
(5)定理4:一组对边平行且相等的四边形是平行四边形。
平行四边形的面积:S=底×高。
考点名称:梯形,梯形的中位线
- 梯形的定义:
一组对边平行,另一组对边不平行的四边形叫做梯形。
梯形中平行的两边叫做梯形的底,通常把较短的底叫做上底,较长的底叫做下底,梯形中不平行的两边叫做梯形的腰,梯形的两底的距离叫做梯形的高。
梯形的中位线:
连结梯形两腰的中点的线段。 梯形性质:
①梯形的上下两底平行;
②梯形的中位线(两腰中点相连的线叫做中位线)平行于两底并且等于上下底和的一半。
③等腰梯形对角线相等。梯形判定:
1.一组对边平行,另一组对边不平行的四边形是梯形。
2.一组对边平行且不相等的四边形是梯形。
梯形中位线定理:
梯形中位线平行于两底,并且等于两底和的一半。
梯形中位线×高= (上底+下底)×高=梯形面积
(上底+下底)×高=梯形面积
梯形中位线到上下底的距离相等
中位线长度= (上底+下底)
(上底+下底)
梯形的周长与面积:
梯形的周长公式:上底+下底+腰+腰,用字母表示:a+b+c+d。
等腰梯形的周长公式:上底+下底+2腰,用字母表示:a+b+2c。
梯形的面积公式:(上底+下底)×高÷2,用字母表示:S=(a+b)×h。
变形1:h=2s÷(a+b);
变形2:a=2s÷h-b;
变形3:b=2s÷h-a。
另一计算梯形的面积公式: 中位线×高,用字母表示:L·h。
对角线互相垂直的梯形面积为:对角线×对角线÷2。梯形的分类:

等腰梯形:两腰相等的梯形。
直角梯形:有一个角是直角的梯形。
等腰梯形的性质:
(1)等腰梯形的同一底边上的两个角相等。
(2)等腰梯形的对角线相等。
(3)等腰梯形是轴对称图形。
等腰梯形的判定:
(1)定义:两腰相等的梯形是等腰梯形
(2)定理:在同一底上的两个角相等的梯形是等腰梯形
(3)对角线相等的梯形是等腰梯形。
- 最新内容
- 相关内容
- 网友推荐
- 图文推荐
| [家长教育] 孩子为什么会和父母感情疏离? (2019-07-14) |
| [教师分享] 给远方姐姐的一封信 (2018-11-07) |
| [教师分享] 伸缩门 (2018-11-07) |
| [教师分享] 回家乡 (2018-11-07) |
| [教师分享] 是风味也是人间 (2018-11-07) |
| [教师分享] 一句格言的启示 (2018-11-07) |
| [教师分享] 无规矩不成方圆 (2018-11-07) |
| [教师分享] 第十届全国教育名家论坛有感(二) (2018-11-07) |
| [教师分享] 贪玩的小狗 (2018-11-07) |
| [教师分享] 未命名文章 (2018-11-07) |