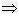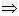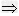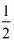题文

已知三整数a，b，c之和为13，且 b a = c b ，求a的最大值和最小值，并求出此时相应的b与c的值．

题型：解答题  难度：中档

答案

设 b a = c b =x，则b=ax，c=ax2，由a+b+c=13化为a（x2+x+1）=13． ∵a≠0， ∴x2+x+1- 13 a =0      ① 又因为a，b，c为整数，则方程①的解必为有理数． 即△=1-4（1- 13 a ）= 52 a -3＞0， 解得1≤a＜ 52 3 ，且 △ 为有理数． 故1≤a≤16 当a=1时，方程①化为x2+x-12=0． 解得x1=-4，x2=3， 故amin=1，b=-4，c=16；amin=1，b=3，c=9． 当a=16时，方程①化为x2+x+ 3 16 =0． 解得x1=- 3 4 ，x2=- 1 4 ． 故amax=16，b=-12，c=9；amax=16，b=-4，c=1．

据专家权威分析，试题“已知三整数a，b，c之和为13，且ba=cb，求a的最大值和最小值，并求..”主要考查你对  一元二次方程根的判别式  等考点的理解。关于这些考点的“档案”如下：

一元二次方程根的判别式

考点名称：一元二次方程根的判别式

• 根的判别式：
  一元二次方程ax²+bx+c=0（a≠0）的根的判别式△=b²-4ac。
  定理1  ax²+bx+c=0（a≠0）中，△＞0方程有两个不等实数根；
  定理2  ax²+bx+c=0（a≠0）中，△=0方程有两个相等实数根；
  定理3  ax²+bx+c=0（a≠0）中，△＜0方程没有实数根。
  
  根的判别式逆用（注意：根据课本“反过来也成立”）得到三个定理。
  定理4  ax²+bx+c=0（a≠0）中，方程有两个不等实数根△＞0；
  定理5  ax²+bx+c=0（a≠0）中，方程有两个相等实数根△＝0；
  定理6  ax²+bx+c=0（a≠0）中，方程没有实数根△＜0。
  注意：（1）再次强调：根的判别式是指△=b²-4ac。
  （2）使用判别式之前一定要先把方程变化为一般形式，以便正确找出a、b、c的值。
  （3）如果说方程，即应当包括有两个不等实根或有两相等实根两种情况，此时b²-4ac≥0切勿丢掉等号。
  （4）根的判别式b²-4ac的使用条件，是在一元二次方程中，而非别的方程中，因此，要注意隐含条件a≠0。

• 根的判别式有以下应用：
  ①不解一元二次方程，判断根的情况。
  ②根据方程根的情况，确定待定系数的取值范围。
  ③证明字母系数方程有实数根或无实数根。
  ④应用根的判别式判断三角形的形状。
  ⑤判断当字母的值为何值时，二次三项是完全平方式。
  ⑥可以判断抛物线与直线有无公共点。
  ⑦可以判断抛物线与x轴有几个交点。
  ⑧利用根的判别式解有关抛物线（△>0）与x轴两交点间的距离的问题。